算法 | 随风

# 牛客

// 模拟readline()函数
function* items() {
    yield '3';
    yield '1 2 3'
}
let num = items();
function readline() {
    return num.next().value;
}
// 无重复最长
const longStr = str => {
    if(str.length === 0) return 0;
    let len = str.length;
    let left = 0;
    let right = 1;
    let max = 0;
    while(right <= len) {
        let lr = str.slice(left, right);
        let index = lr.indexOf(str[right]);
        if (index > -1) {
            left = left + index + 1;
        } else {
            lr = str.slice(left, right + 1);
            max = Math.max(max, lr.length)
        }
        right++
    }
    return max;
}
var str = readline() // 使用readline()读取
console.log(longStr(str))

// 公共子串
const fun = () => {
    let line
    while(line = readline()) {
        let str1 = line
        let str2 = readline()
        let count = 0
        for(let i=0;i<=line.length;i++) {
            for(let j=i;j<=line.length;j++) {
                let str = line.substring(i,j)
                if(str2.indexOf(str)>-1){
                    if(count<str.length) {
                        count = str.length
                    }
                }
            }
        }
        console.log(count)
    }
}
fun()

// 购物清单
// 输入：
// 50 5
// 20 3 5
// 20 3 5
// 10 3 0
// 10 2 0
// 10 1 0
// 输出：
// 130
// 说明：
// 由第1行可知总钱数N为50以及希望购买的物品个数m为5；
// 第2和第3行的q为5，说明它们都是编号为5的物品的附件；
// 第4~6行的q都为0，说明它们都是主件，它们的编号依次为3~5；
// 所以物品的价格与重要度乘积的总和的最大值为10*1+20*3+20*3=130       
let line1 = readline()
const n = parseInt(line1.split(' ')[0]); // 自己拥有的钱
const m = parseInt(line1.split(' ')[1]); // 自己可以买多少物品
const v = [''], w = [''], s = ['']
let index = 0 //用于接收输入的数组
while(index < m) {
    let line = readline().split(' ')
    v.push(parseInt(line[0]))  //每件物品的价格
    w.push(parseInt(line[1]))  //每件物品的满意度
    s.push(parseInt(line[2])) //每件物品是否为主件
    index++
}
//构建dp数组
//构建二维dp数组，横坐标为自己买的物品数目，纵坐标为自己花费的价格，全部初始化为0
const solve = (n, m, v, w, s) => {
    const dp = new Array(m+1).fill(0).map(() => new Array(n+1).fill(0))
    let res = 0
    for(let i=1;i<=m;i++) { //横坐标逐渐增加的过程，模拟自己的钱越来越多
        for(let j=0;j<=n;j++) { //纵坐标逐渐增加的过程，模拟自己能买物品的数量越来越多
            //如果是正常的背包问题现在套用公式即可，但是现在添加的是否为主副件
            if (!s[i]) { //如果现在是主件
                if(j >= v[i]){ // 现有金额满足购买
                    const sub = [] // 收集主件后的附件
                    for (let k=1;k<=s.length;k++) {
                        if (s[k] == i) sub.push(k) // 这个主件有几个附件，就以1，2的形式push进数组
                    }
                     //在没有附件的情况下就是套用背包公式dp数组
                    dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j - v[i]] + w[i]*v[i])
                    //之后分类讨论，因为题目说了只有1，2附件就依次写出来
                    //如果有一个附件，比较是否买
                    if(sub[0] && j>= v[i]+v[sub[0]]) {
                        //判断是否买不买这件物品，还是基于背包公式的else部分
                        dp[i][j] = Math.max(dp[i][j], dp[i-1][j - v[i] - v[sub[0]]] + w[i]*v[i] + w[sub[0]] * v[sub[0]])
                    }
                    if(sub[1] && j>= v[i]+v[sub[1]]) {
                          //如果有两个附件，比较是否买（注意是if依次判断）
                        dp[i][j] = Math.max(dp[i][j], dp[i-1][j - v[i] - v[sub[1]]] + w[i]*v[i] + w[sub[1]] * v[sub[1]])
                    }
                    // 如果还有空余
                    if (sub.length == 2 && j>= v[i]+v[sub[1]]+v[sub[0]]) {
                        dp[i][j] = Math.max(dp[i][j], dp[i-1][j-v[i]-v[sub[0]]-v[sub[1]]] +w[i]*v[i]+w[sub[1]] * v[sub[1]]+w[sub[0]] * v[sub[0]])
                    }
                    res = Math.max(res, dp[i][j])
                } else dp[i][j] = dp[i-1][j]  //不要放进去
            } else dp[i][j] = dp[i-1][j]  //不要放进去
        }
    }
    return res
}
console.log(solve(n,m,v,w,s))

最长公共子序列

最长公共子串

购物清单 (opens new window)

// 尼科彻斯定理 输入：6  输出：31+33+35+37+39+41
//规律：最后一个数为：num的平方+num-1，第一个数为：num的平方-num-1
    // 1:1-0
    // 2:4-1
    // 3:9-2
    // 4:16-3
    // 5:25-4
    // 6:36-5
let line = parseInt(readline());
let start = line * (line - 1) + 1;
let res = [];
for(let i = 0; i < line; i++) {
    res.push(start + i * 2)
}
return res.join('+')

# 找出数组的最大公约数

// 输入：nums = [2,5,6,9,10]
// 输出：2
// 解释：
// nums 中最小的数是 2
// nums 中最大的数是 10
// 2 和 10 的最大公约数是 2
const findGCD = nums => {
    let min = Math.min(...nums);
    let max = Math.max(...nums);
    if(max % min === 0) return min;
    for(let i = min; i>= 0; i--) {
        if(min % i === 0 && max % i === 0) return i;
    }
}

序列中不同最大公约数的数目 (opens new window)

# 正则表达式匹配

给你一个字符串s和一个字符规律p，请你来实现一个支持'.'和'*'的正则表达式匹配

'.'匹配任意单个字符
'*'匹配另个或多个签名的那一个元素所谓匹配，是要涵盖整个字符串s的，而不是部分字符串

输入：s = "aa", p = "a"
输出：false
解释："a" 无法匹配 "aa" 整个字符串。

输入：s = "aa", p = "a*"
输出：true
解释：因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此，字符串 "aa" 可被视为 'a' 重复了一次。


输入：s = "ab", p = ".*"
输出：true
解释：".*" 表示可匹配零个或多个（'*'）任意字符（'.'）。

解答

var isMatch = function(s, p) {
    if(s === null || p === null) return false;
    const sLen = s.length;
    const pLen = p.length;
    const dp = Array.from(Array(sLen + 1), (_, i) => Array(pLen + 1).fill(false));
    // base case
    dp[0][0] = true;
    for (let j = 1; j < pLen + 1; j++) {
        if (p[j - 1] === '*') dp[0][j] = dp[0][j - 2];
    }
    // 迭代
    for(let i = 1; i < sLen + 1; i++) {
        for (let j = 1; j < pLen + 1; j++) {
            if (s[i - 1] == p[j - 1] || p[j - 1] == ".") {
                dp[i][j] = dp[i - 1][j - 1];
            } else if(p[j - 1] === '*') {
                if (s[i - 1] == p[j - 2] || p[j - 2] == ".") {
                    dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 2] || dp[i - 1][j];
                } else {
                    dp[i][j] = dp[i][j - 2];
                }
            }
        }
    }
    return dp[sLen][pLen];
};
// 第二种
function isMatch(s, p) {
  var lenS = s.length;
  var lenP = p.length;
  var map = {};

  return check(0, 0);

  function check(idxS, idxP) {
    if (map[idxS + ':' + idxP] !== undefined) return map[idxS + ':' + idxP];
    if (idxS > lenS) return false;
    if (idxS === lenS && idxP === lenP) return true;

    if (p[idxP] === '.' || p[idxP] === s[idxS]) {
      map[idxS + ':' + idxP] = p[idxP + 1] === '*' ?
        check(idxS + 1, idxP) || check(idxS, idxP + 2) :
        check(idxS + 1, idxP + 1);
    } else {
      map[idxS + ':' + idxP] = p[idxP + 1] === '*' ?
        check(idxS, idxP + 2) : false;
    }
    return map[idxS + ':' + idxP];
  }
}

# 两数之和

var twoSum = function(nums, target) {
    let obj = {};
    for (let i = 0; i < nums.length; i++) {
        num = nums[i];
        if (num in obj) {
            return [obj[num], i];
        } else {
            obj[target - num] = i
        }
    }
}
// 第二种
function twoSum(nums, target) {
  for (let i = 0; i < nums.length; i++) {
    let right = i + 1;
    while(right < nums.length) {
      let sum = nums[i] + nums[right];
      if (sum === target) {
        return [i, right];
      } else {
        right++;
      }
    }
  }
}
twoSum([2,7,11,16], 9)

# 三数之和

var threeSum = function(nums) {
    let ans = [];
    const len = nums.length;
    if(nums == null || len < 3) return ans; // 注意这句 比较重要
    nums.sort((a, b) => a - b); // 排序
    for (let i = 0; i < len ; i++) {
        if(nums[i] > 0) break; // 如果当前数字大于0，则三数之和一定大于0，所以结束循环
        if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
        let L = i+1;
        let R = len-1;
        while(L < R){
            const sum = nums[i] + nums[L] + nums[R];
            if(sum == 0){
                ans.push([nums[i],nums[L],nums[R]]);
                while (L<R && nums[L] == nums[L+1]) L++; // 去重
                while (L<R && nums[R] == nums[R-1]) R--; // 去重
                L++;
                R--;
            }
            else if (sum < 0) L++;
            else if (sum > 0) R--;
        }
    }        
    return ans;
};
var nums = [-1, 0, 1, 2, -1, -4]
console.log(threeSum(nums));

力扣三数之和 (opens new window)

# 快排

# 阮一峰老师的js快排实现

选择数组中间数作为基数，并从数组中取出此基数
准备两个数组容器，遍历数组，逐个与基数比对，较小的放左容器，较大的放右容器
递归处理两个容器的元素，并将处理后的数据与基数按大小合并成一个数组返回

var quickSort = function(arr) {
    if (arr.length <= 1) return arr; // 设置边界
    var pivotIndex = Math.floor(arr.length / 2);
    var pivot = arr.splice(pivotIndex, 1)[0];
    var left = [];
    var right = [];
    for (var i = 0; i < arr.length; i++) { // 需要注意 arr.length 需要splice之后获取
        if (arr[i] < pivot) {
            left.push(arr[i]);
        } else {
            right.push(arr[i]);
        }
    }
    return quickSort(left).concat([pivot], quickSort(right));
}

总结

思路非常清晰，选择基数作为参照，划分数组,分而治之，对于新手来理解快排的核心思想"参照-划分-递归"，很容易理解

既实现了排序，又符合快速排序的思想，为什么还会有人诟病呢，是因为：

取基数用的是splice()函数取，而不是算法中常用的取下标。基数只是一个参照对象，在比对的时候，只要能从数组中取到就好，所以只需要知道它的索引，调用函数删除基数只会更耗时。
根据基数来划分时,专门生成两个数组来存储，从而占用更多的存储空间(增加了空间复杂度)

严格来讲，还有更多改进之处

# 文章中提出的快排js实现

思路：

1、通过下标取中间数为基数；

2、从起点往后寻找比基数大的，记录为下标 i；再从终点往前寻找比基数小的，记录为下标 j，当 i <= j时，原地交换数值；

3、重复步骤2，直到遍历所有元素，并记录遍历的最后一个下标 i，以此下标为分界线，分为左右两边，分别重复步骤1~3实现递归排序；

实现（为方便理解，在原文基础上有所合并）：

// 快排改进——黄佳新
var devide_Xin = function (array, start, end) {
    if(start >= end) return array;
    var baseIndex = Math.floor((start + end) / 2), // 基数索引
            i = start,
            j = end;

    while (i <= j) {
        while (array[i] < array[baseIndex]) {
            i++;
        }
        while (array[j] > array[baseIndex])  {
            j--;
        }

        if(i <= j) {
            var temp = array[i];
            array[i] = array[j];
            array[j] = temp;
            i++;
            j--;
        }
    }
    return i;
}

var quickSort_Xin = function (array, start, end) {
    if(array.length < 1) {
        return array;
    }
    var index = devide_Xin(array, start, end);
    if(start < index -1) {
        quickSort_Xin(array, start, index - 1);
    }
    if(end > index) {
        quickSort_Xin(array, index, end);
    }

    return array;
}

总结：

1、用下标取基数，只有一个赋值操作，跟快；

2、原地交换，不需要新建多余的数组容器存储被划分的数据，节省存储；

比较：

相较而言，理论分析，实现二确实是更快速更省空间，那么事实呢？

耗时比较

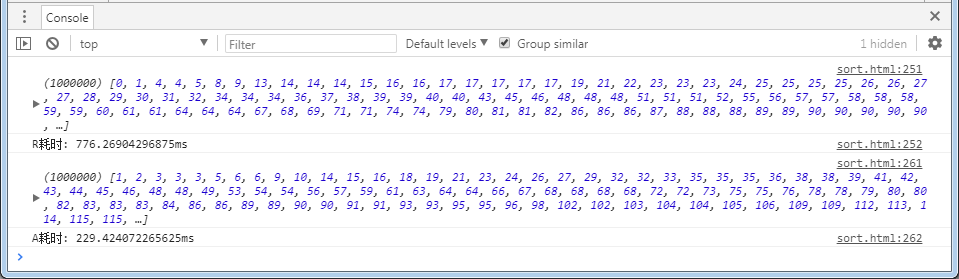
以上是实现一与实现二在chrome上测试耗时的统计结果，测试方案为：各自随机生成100万个数（乱序）,分别完成排序，统计耗时。

结论：

事实上，乱序排序，实现二更快。

# 三、网上其他的快排js实现

思路：

1、通过下表取排序区间的第0个数为基数

2、排序区间基数以后，从右往左，寻找比基数小的，从左往右，寻找比基数大的，原地交换；

3、重复步骤2直到 i >= j；

4、将基数与下标为 i 的元素原地交换，从而实现划分；

5、递归排序基数左边的数，递归排序基数右边的数，返回数组。

var quickSort_New = function(ary, left, right) {
    if(left >= right) {
        return ary;
    }

    var i = left,
            j = right;
            base = ary[left];

    while (i < j) {
        // 从右边起，寻找比基数小的数
        while (i<j && ary[j] >= base) {
            j--;
        }

        // 从左边起，寻找比基数大的数
        while (i<j && ary[i] <= base) {
            i++
        } 

        if (i<j) {
            var temp = ary[i];
            ary[i] = ary[j];
            ary[j] = temp;
        }
    }

    ary[left] = ary[i];
    ary[i] = base;

    quickSort_New(ary, left, i-1);
    quickSort_New(ary, i+1, right);

    return ary;
}

总结：

除选基数不同以外，其他与实现二类似。

另外：

比较一下实现二与实现三的速度，结果如下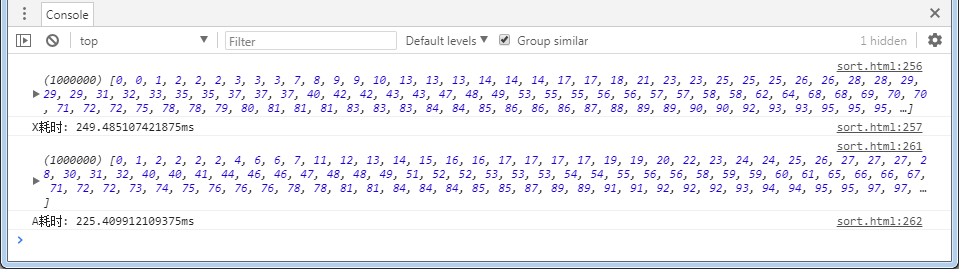： foo 多次测试结果均为：实现二耗时略小于实现三，偶尔出现大于的情况，但相差不大。

# 二分查找

function binary_search(arr, low, high, key) {
    if (low > high) retrun -1;
    var mid = parseInt((low + high) / 2);
    if (arr[mid] === key) {
        return mid;
    } else if (arr[mid] > key) {
        high = mid - 1;
        return binary_search(arr, low, high, key);
    } else if (arr[mid] < key) {
        low = mid + 1;
        return binary_search(arr, low, high, key);
    }
}

第二种

var search = function(nums, target) {
    let left = 0;
    let right = nums.length - 1;
    while(left <= right) {
        let mid = Math.floor((left + right) / 2);
        console.log(mid)
        if(nums[mid] === target) {
            return mid;
        }
        if (nums[mid] > target) {
            right = mid - 1;
        }
        if (nums[mid] < target) {
            left = mid + 1;
        }
    }
    return -1;
}

// 给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。
// 请必须使用时间复杂度为 O(log n) 的算法
//  nums = [1,3,5,6], target = 5 输出: 2
//  nums = [1,3,5,6], target = 7 输出5
const searchInsert = (nums, target) => {
    let n = nums.lenght;
    let left = 0, right = n - 1;
    let ans = n;
    while(left <= right) {
        let mid = (left + right) >> 1;
        if(target <= nums[mid]) {
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

第三种

// 整数数组 nums 按升序排列，数组中的值 互不相同 。

// 在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

// 给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

// 输入：nums = [4,5,6,7,0,1,2], target = 0
// 输出：4
var search = function(nums, target) {
    // return nums.indexOf(target)
    let left = 0;
    let right = nums.length - 1;
    while(left <= right) {
        let mid = Math.floor((left + right) / 2);
        if(nums[mid] === target) {
            return mid;
        }
        if(nums[left] <= nums[mid]) {
            if(nums[left] <= target && target <= nums[mid]) {
                right = mid - 1;
            } else {
                left = mid + 1;
            }
        } else {
            if(nums[mid] <= target && target <= nums[right]) {
                left = mid + 1;
            } else {
                right = mid -1
            }
        }
    }
    return -1;
};
console.log(search([4,5,6,7,0,1,2], 0))

# 扑克牌问题

魔术师手中有一堆扑克牌，观众不知道它的顺序，接下来魔术师：

从牌顶拿出一张牌，放到桌子上再从牌顶拿一张牌，放在手上牌的底部如此往复（不断重复以上两步），直到魔术师手上的牌全部都放到了桌子上。

此时，桌子上的牌顺序为： (牌顶) 1,2,3,4,5,6,7,8,9,10,11,12,13 (牌底)。

问：原来魔术师手上牌的顺序，用函数实现。

function getOrigin(nums = []) {
    let result = [];
    while (nums.length) {
        if (result.length > 1) result.unshift(result.pop());
        result.unshift(nums.shift());
    }
    return result;
}
// [13, 2, 12, 6, 11, 3,10, 5,  9, 1,  8, 4,7]

扑克牌问题 (opens new window)

# 有A、B两个数组

A: [1,2,3,4,5]

B: [5,1,4,2,3]

function formatArr(nums) {
    let arr = [];
    while(nums.length > 0) {
        if (arr.length % 2 === 1) {
            arr.push(nums.shift());
        } else {
            arr.push(nums.pop())
        }
    }
    return arr;
}
console.log(formatArr([1,2,3,4,5]))

洗牌函数

# JavaScript 深拷贝

//简单
function copyObj(obj) {
    var newobj = {};
    for(const key in obj) {
        if(typeof obj[key] === 'object') {
            newobj[key] = copyObj(obj[key])
        } else {
            newobj[key] = obj[key]
        }
    }
    return newobj;
}
// 数组对象
  const deepClone = obj => {
      let newobj = obj.constructor  === Array ? [] : {};
      for(let key in obj) {
          if(typeof obj[key] === 'object') {
              newobj[key] = deepClone(obj[key]);
          } else {
              newobj[key] = obj[key];
          }
      }
      return newobj;
  }
  console.log(deepClone({a: 1, b: 2, c:[2, 3, 4, [4, 5, 6, { a: 1, b: 2 }]]}))

/** MessageChannel接口允许创建一个新的消息通道，并通过它的两个MessagePort属性发送数据。MessageChannel接口实例化以后，会有两个属性port1和port2.**/
function copyObj(obj) {
    return new Promise(resolve => {
        const { port1, port2 } = new MessageChannel();
        port1.postMessage(obj);
        port2.onmessage = ev => resolve(ev.data);
    })
}
var obj1 = {a:1}
var clone1 = await structuralClone(obj1)

深拷贝的实现，如果遇到function怎么办-3

对象循环引用问题

对象copy

# 盛水最多的容器---双指针法

var maxArea = function(height) {
  let left = 0;//左下标
  let right = height.length - 1;//右下标
  let max = 0;//最大装水量
  while(left < right){
      let now = (right - left) * Math.min(height[right], height[left]);
      max = now > max ? now : max;
      if(height[left] > height[right]){
          right--;
      }else{
          left++;
      }
  }
  return max;
};

leecode (opens new window)

# 接雨水

给定n个非负整数表示每个宽度为1的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水接雨水

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出：6
解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

解答：

var trap = function(height) {
    let ans = 0;
    let left = 0, right = height.length - 1;
    let leftMax = 0, rightMax = 0;
    while (left < right) {
        leftMax = Math.max(leftMax, height[left]);
        rightMax = Math.max(rightMax, height[right]);
        if (height[left] < height[right]) {
            ans += leftMax - height[left];
            left++;
        } else {
            ans += rightMax - height[right];
            right--;
        }
    }
    return ans;
};
// 单调栈
let trap = function(height) {
    let ans = 0;
    const stack = [];
    const n = height.length;
    for(let i = 0; i < n; i++) {
        while(stack.length && height[i] > height[stack[stack.length - 1]]) {
            const top = stack.pop();
            if(!stack.length) break;
            const left = stack[stack.length - 1];
            const currWidth = i - left - 1;
            const currHeight = Math.min(height[left], height[i]) - height[top]; // 面积 可能左侧的更小...
            ans += currWidth * currHeight;
        }
        stack.push(i);
    }
    return ans;
}

leetcode (opens new window)

# 大数相加--双指针

思路遍历两个字符串从个位数算起开始相加，定义temp接受两个数之和，除以10取余拼接上结果，最后判断temp是否大于0，如果大于9则进位temp=1

var addstring = function(num1, num2) {
    var len1 = num1.length, len2 = num2.length; temp = 0; res = '';
    while(len1 || len2) {
        if(len1) {
            temp += +num1[--len1];
        }
        if(len2) {
            temp += +num2[--len2];
        }
        res  = temp % 10 +res;
        if(temp > 9) {
            temp =1;
        } else {
            temp = 0;
        }
    }
    if (temp) {
        res = 1 +res; 
    }
    return res;
}

类似算法题

交替合并字符串 (opens new window)

// 输入：word1 = "abc", word2 = "pqr"
// 输出："apbqcr"
// 解释：字符串合并情况如下所示：
// word1：  a   b   c
// word2：    p   q   r
// 合并后：  a p b q c r
var mergeAlternately = function(word1, word2) {
    const m = word1.length, n = word2.length;
    let i = 0, j = 0;

    const ans = [];
    while (i < m || j < n) {
        if (i < m) {
            ans.push(word1[i]);
            ++i;
        }
        if (j < n) {
            ans.push(word2[j]);
            ++j;
        }
    }
    return ans.join('');
};

# sqrt---平方根

var mySqrt = function(x) {
     if (x < 2) return x
     let left = 1, mid, right = Math.floor(x / 2);
     while (left <= right) {
        mid = Math.floor(left + (right - left) / 2)
        if (mid * mid === x) return mid
        if (mid * mid < x) {
            left = mid + 1
        }else {
            right = mid - 1
        }
     }
     return right
};

# 立方根

let num = readline();
function fn(res) {
    return res < 0 ? Math.cbrt(res).toFixed(1) : Math.pow(res, 1/3).toFixed(1);
}
console.log(fn(num))

// 递归求解
let str=readline()
let num=0
function cal(str){
    str=Math.abs(str)
    if(num*num*num<=str){
        num+=0.01
        cal(str)
    }
    return num
}
cal(str)
console.log(str>=0?num.toFixed(1):-num.toFixed(1))

// 二分
const val = parseFloat(readline());
 
function bs(v) { 
  const sign = v >= 0 ? 1 : -1;
  v = Math.abs(v);
  let left = 0, right = Math.max(v, 1);
  let mid;
  while (right - left > 1e-5) {
    mid = (right + left) / 2;
    if (v - mid * mid * mid > 0) {
      left = mid;
    } else {
      right = mid;
    }
  }
  return sign * mid;
}
const rv =bs(val).toFixed(1);
console.log(rv);

# [动态规划]恢复空格

哦，不！你不小心把一个长篇文章中的空格、标点都删掉了，并且大写也弄成了小写。像句子"I reset the computer.It still didn't boot!"已经变成'iresetthecomputeritstilldidntboot'。在处理标点符号和大小写之前，你得先把它断成词语。当然了，你有一本厚厚的词典dictionary,不过有些词没在词典里。假设文章用sentence表示，设计一个是算法，把文章断开，要求未识别的字符最少，返回未识别的字符数。

注意：本题对原题稍作改动，只需返回未识别的字符数

//示例
输入：dictionary = ['looked', 'just', 'like', 'her', 'brother'];
sentence = 'jesslookedjustliketimherbrother';
输出 7
解释：断句后'jess looked just like tim her brother',共7个未识别字符。

var respace = function(dictionary, sentence) {
     if(sentence.length == 0) return 0;
    let dp = new Array(sentence.length).fill(0);
    for(let i = 1;i<=sentence.length;i++){
        dp[i] = dp[i-1]+1;
        // 上面表示，如果没有匹配那么dp[i]相比于dp[i-1]直接多1
        // 接着讨论如果新加一个字符，组成了一个词的情况
        for(let j=0;j<dictionary.length;j++){
            let word = dictionary[j].length;
            if(dictionary[j] == sentence.substring(i-word,i) && word<=i){
                dp[i] = Math.min(dp[i],dp[i-word]);
            }
        }
    }
    return dp[sentence.length]
};

# 两个数组的交集

/**
给定两个数组，编写一个函数来计算它们的交集。
示例1：
输入：nums1 = [1,2,2,1], num2 = [2,2];
输出： [2,2]
说明：
   输出结果中每个元素出现的次数，应与元素在两个数组中出现的次数一致
   我们可以不用考虑输出结果的顺序
**/
var intersect = function(nums1, nums2) {
    let tmp = [], arr = [];
    if(nums1.length > nums2.length) {
        tmp = nums1;
        nums1 = nums2;
        nums2 = tmp;
    }
    for (let key of nums1) {
        temp = nums2.indexOf(key);
        if(temp > -1) {
            arr.push(key);
            nums2.splice(temp, 1);
        }
    } 
    return arr;
}


// 交集并集差集
  var set1 = new Set([1,2,3]);
  var set2 = new Set([2,3,4]);

  并集
  let union = new Set([...set1, ...set2]);

  交集
  let intersect = new Set([...set1].filter( x => set2.has(x)));

  差集
  let difference = new Set([...set1].filter(x => !set2.has(x)));

参考 (opens new window)

多个数组交集

# 统计字符串出现最多的字符

function getMax(str) {
    var hash = {}, maxStr, max = 1;
    for (var i = 0; i < str.length; i++) {
        if (!hash[str[i]]){
            hash[str[i]] = 1;
        } else {
            hash[str[i]]++;
        }
        if (hash[str[i]] > max) {
            max = hash[str[i]];
            maxstr = str[i];
        }
    }
    return masStr;
}

# 无重复字符的最长子串--单指针

参考

var getSubString = function(str) {
    if (!str.length) return 0;
    let tempStr = '';
    let maxStrlen = 0;
    let len = str.length;
    let left = 0;
    for (var i = 0; i < len; i++) {
        if (tempStr.indexOf(str[i]) !== -1) {
            left += (str.slice(left, i)).indexOf(str[i]) + 1;
            continue;
        }
        tempStr = str.slice(left, i + 1);
        maxStrlen = Math.max(maxStrlen, tempStr.length);
    }
    return maxStrlen
}
// 第二种
var lengthOfLongestSubstring = function(s) {
    const map = {};
    let left = 0;
    return s.split('').reduce((max, v, i) => {
        left = map[v] >= left ? map[v] + 1 : left;
        map[v] = i;
        return Math.max(max, i - left + 1);
    }, 0)
};

// 最长字符串
const longstr = str => {
    let left = 0;
    let map = {}
    let temp = '';
    let max = 0;
    max = str.split('').reduce((max, v, i) => {
        left = map[v] >= left ? map[v] + 1 : left;
        map[v] = i;
        if(i - left + 1 > max) {
            temp = str.substring(left, i + 1)
            max = i - left + 1;
        }
        return max;
    }, 0)
    return temp;
}
console.log(longstr('fdasfasf'))

# z-字形变换

将一个给定字符串 s 根据给定的行数 numRows ，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 "PAYPALISHIRING" 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如："PAHNAPLSIIGYIR"。

请你实现这个将字符串进行指定行数变换的函数：

string convert(string s, int numRows);

解决

var convert = function(s, numRows) {
     // return original string if can't zigzag
     if (numRows === 1 || s.length < numRows) return s;

     let rows = []
     let reverse = false;
     let count = 0
 
     // prepare rows
     for (let i = 0; i < numRows; i++) rows[i] = [];
     // reverse the push flow when reaching turning points
     for (let i = 0; i < s.length; i++) {
         rows[count].push(s[i]);
         reverse ? count-- : count++;
         if (count === numRows - 1 || count === 0) reverse = !reverse;
     }
     // put together converted string
     return rows.reduce((converted, cur) => converted + cur.join(''), '');
};

# 查找一个字符中指定的子串的所有位置

var str = 'fdhfgcsaedvcfhgfh';
var index = str.indexOf('f'); // 字符出现的位置
var num = 0; // 这个字符出现的次数

while(index !== -1){
    console.log(index);
    num++;
    index = str.indexOf('f', index + 1); // 从字符串出现的位置的下一个位置开始继续查找
}
console.log('f一共出现了'+num+'次');

# 缺失的第一个正数

TIP

给一个未排序的正数数组，找出没有出现的最小正正数

[1,2,0] => 3

[3, 4, -1, 1] => 2

[7, 8, 9,11, 12] => 1

var firstMissingPositive = function(nums) {
    let result = 1;
    while(nums.includes(result)) {
        result++;
    }
    return result;
}

# 寻找两个正序数组的中位数

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

const findMedianSortedArrays = (nums1, nums2) => {
    const newArr = [...nums1, ...nums2].sort((a, b) => a - b);
    let result = 0;
    if(newArray.length / 2 === parseInt(newArr.length / 2)) {
        result = (newArr[parseInt(newArr.length / 2)] + newArr[parseInt(newArr.length / 2) - 1]) / 2;
    } else {
        result = newArr[parseInt(newArr.length / 2)]
    }
    return result;
}

leetcode (opens new window)

# [数组]JS获取数组的所有子集---重要

// 使用js获取一个数组的所有子集,如：[1,2,3]所有子集[[], [1], [2], [3], [1, 2], [1, 3], [2, 3], [1, 2, 3]]

// 思路:假设res是一个二维空数组[[]]，遍历原数组arr,给当前结果res中的每一个子数组append arr[i],得到tempRes[[1]],在把得到的结果加入到res当中，res变成[[], [1]]，一次类推
function allSubsets(arr) {
    let res = [[]];
    for(let i = 0; i < arr.length; i++) {
        const tempRes = res.map(item => {
            const one = item.concat([]);
            one.push(arr[i]);
            return one;
        })
        res = res.concat(tempRes);
    }
    return res;
}
// 第二种
function allSubsets(nums) {
    return nums.reduce((acc, cur) => {
        return acc.concat(acc.map(v => [cur, ...v]))
    }, [[]])
}
allSubsets([1,2,3]); // [[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

获取数组的子集数组 (opens new window)

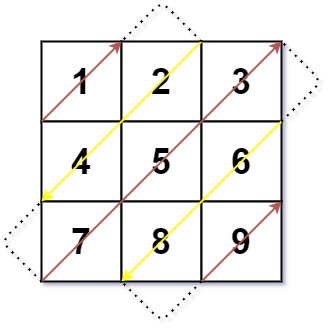
# [数组]对角线遍历

对角线遍历

const findDiagonaOrder = mat => {
    const row = mat.length
    const col = mat[0].length
    const record = new Map()
    for (let i = 0; i < row; i++) {
        for (let j = 0; j < col; j++) {
        const key = i + j
        if (!record.has(key)) record.set(key, [])
        record.get(key).push(mat[i][j])
        }
    }

    const res = []
    for (const [key, nums] of record.entries()) {
        key % 2 === 1 ? res.push(...nums) : res.push(...nums.reverse())
    }


    return res
}

leetcode (opens new window)

# [数组]对角线遍历 II

给你一个列表 nums ，里面每一个元素都是一个整数列表。请你依照下面各图的规则，按顺序返回 nums 中对角线上的整数。对角线遍历

输入：nums = [[1,2,3],[4,5,6],[7,8,9]]
输出：[1,4,2,7,5,3,8,6,9]

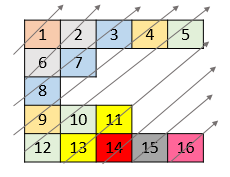
对角线遍历

输入：nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
输出：[1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]

解答

const findDiagonaOrder = nums => {
    if (nums.length === 0) return [];
    let arrays = [], result = [];
    // 根据下标和聚类
    for(let i = 0; i < nums.length; i++) {
        let rows = nums[i];
        for (let j = 0; j < rows.length;j++) {
            if (!arrays[i + j]) arrays[i + j] = [];
            arrays[i + j].push(nums[i][j]);
        }
    }
    // 二维数组扁平化
    for(const rows of arrays) {
        result.push(...rows.reverse())
    }
    return result;
}

leetcode (opens new window)

# [数组]合并区间

以数组 intervals 表示若干个区间的集合，其中单个区间为 intervals[i] = [starti, endi] 。请你合并所有重叠的区间，并返回一个不重叠的区间数组，该数组需恰好覆盖输入中的所有区间。

输入：intervals = [[1,3],[2,6],[8,10],[15,18]]
输出：[[1,6],[8,10],[15,18]]
解释：区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].

解答

const merge = intervals => {
    // 先按第一个元素排序
    intervals.sort((a, b) => a[0] - b[0])

    // 计算合并
    let res = []
    for (let i = 1; i < intervals.length; i++) {
        // 对于 [1,3] 和 [2,6], 比较 3 和 2, 3 >= 2 则合并
        if (intervals[i][0] <= intervals[i - 1][1])
            intervals[i] = [intervals[i - 1][0], Math.max(intervals[i - 1][1], intervals[i][1])]
        else
            // 不能合并则将上一个合并结果加入 
            res.push(intervals[i - 1])
    }
    // 最后一次的结果需要额外放入
    res.push(intervals[intervals.length - 1])
    return res
}

# [数组]汇总区间

// 输入：nums = [0,1,2,4,5,7]
// 输出：["0->2","4->5","7"]
// 解释：区间范围是：
// [0,2] --> "0->2"
// [4,5] --> "4->5"
// [7,7] --> "7"
const summaryRanges = nums => {
    const ret = [];
    let i = 0;
    const n = nums.length;
    while(i < n) {
        let low = i;
        i++;
        while(i < n && nums[i] === nums[i - 1] + 1) {
            i++;
        }
        let high = i - 1;
        let temp = ['' + nums[low]];
        if(low < high) {
            temp.push('->');
            temp.push('' + nums[high])
        }
        ret.push(temp.join(''))
    }
    return ret;
}
// 双指针
function summaryRanges(nums) {
    let ans = [];
    let last = nums[0];
    let start = nums[0];
    for(let i of nums.keys()) {
        let num = nums[i + 1];
        if(num != last + 1) {
            if(last === start) {
                ans.push(String(last));
            } else {
                ans.push([start, last].join('->'));
            }
            start = num;
        }
        last = num;
    }
    return ans;
}

汇总区间 (opens new window)

# [数组]缺失区间

const lackOfInterval = (nums, lower, upper) => {
    const res = [];
    nums.push(upper + 1);
    nums.unshift(lower - 1);
    for(let num of nums) {
        if(num === lower + 2) {
            res.push(`${lower + 1}`)
        } else if(num > lower + 2) {
            res.push(`${lower + 1}->${num - 1}`)
        }
        lower = num;
    }
    return res;
}
console.log(lackOfInterval([0, 1,3,50, 74], 0 , 99)) // [2, '4->49', '51->73', '74-> 99']

# [数组]除自身以外的数组的乘积

输入: nums = [1,2,3,4]
输出: [24,12,8,6]

解答

const productExceptSelf = nums => {
    const n = nums.length;
    const output = [];
    output[0] = 1;
    for (let i = 1; i < n; i++) { // output[i]是nums[i]的左编辑
        output[i] = output[i - 1] * nums[i - 1];
    }
    let right_output = 1; // 保存nums[i]的左边积
    for(let i = n - 1; i >= 0; i--) {
        output[i] *= right_output // 左边积 乘上 右边积
        right_output *= nums[i]; // 更新右边积
    }
    return output;
}

leetcode (opens new window)

# 数组中的第K个最大元素

输入: [3,2,1,5,6,4] 和 k = 2

输出: 5

使用堆排序来解决这个问题——建立一个大顶堆，做k−1 次删除操作后,堆顶元素就是我们要找的答案（堆排序过程中，不全部下沉，下沉nums.length-k+1,然后堆顶可以拿到我们top k答案了）

首先构建一个大顶堆
获取数组减去K 之后的重新构建大顶堆
大顶堆最上面的就是

// 第一种
var findKthLargest = function(nums, k) {
    nums = nums.sort((a, b) => a -b);
    return nums[k - 1]
}
// 堆排序--大顶堆
//整个流程就是上浮下沉
var findKthLargest = function(nums, k) {
  let heapSize = nums.length;
  buildMaxHeap(nums, heapSize); // 构建好了一个大顶堆
  // 进行下沉 大顶堆是最大元素下沉到末尾
  for(let i = nums.length - 1; i >= nums.length - k + 1; i--) {
    swap(nums, 0, i);
    --heapSize; // 下沉后的元素不参与到大顶堆的调整
    // 重新调整大顶堆
    maxHeapify(nums, 0, heapSize);
  }
  return nums[0];
  
  // 自下而上构建一个大顶堆
  function buildMaxHeap(nums, heapSize) {
    for (let i = Math.floor(heapSize / 2) - 1; i >= 0; i--) {
      maxHeapify(nums, i, heapSize);
    }
  }
  // 从左向右，自上而下的调整节点
  function maxHeapify(nums, i, heapSize) {
    let l = i * 2 + 1;
    let r = i * 2 + 2;
    let largest = i;
    if (l < heapSize && nums[l] > nums[largest]) {
      largest = l;
    }
    if (r < heapSize && nums[r] > nums[largest]) {
      largest = r;
    }
    if (largest !== i) {
      swap(nums, i, largest); // 进行节点调整
      // 继续调整下面的非叶子节点
      maxHeapify(nums, largest, heapSize)
    }
  }
  function swap(a, i, j) {
    let temp = a[i];
    a[i] = a[j];
    a[j] = temp;
  }
}

总结-JS数据结构与常用算法

力扣官方 (opens new window)

数组中的第K个最大元素 (opens new window)

coding-堆

# [数组]最大序数和/连续子数组的最大值

var maxSubArray = function(nums) {
    var cur = 0; maxSub = nums[0];
    nums.forEach(x => {
        cur = Math.max(cur + x, x);
        maxSub = Math.max(maxSub, cur);
    })
    return maxSub;
};
var arr = [1,2,3, 1,3,4, -19, 34,-23];
console.log(masSubArray(arr)); // 34

leetcode (opens new window)

# [数组]长度最小的子数组(掌握滑动窗口&指针)

给定一个含有 n 个正整数的数组和一个正整数 target 。

TIP

s = 7； nums = [2, 3,1, 2, 4, 3];

输出2，子数组[4, 3] 最小的连续子数组

var minSubArrayLen = function(s, nums) {
    let n = nums.length;
    let left = 0, res = Infinity, sum = 0;
    for (let right = 0; right < n; right++) {
        //记录和
        sum += nums[right];
        //满足条件,收缩左指针
        while(sum >= s) {
            //收缩之前，取最小值  
            res = Math.min(res, right - left + 1);
            sum -= nums[left++];
        }
    }
    //注意数组全部加起来或者数组为0的时候，res不变；
    return res == Infinity ? 0 : res;
}
// 方法二 等同一？
var minSubArrayLen = function(target, nums) {
    const n = nums.length;
    
    // S1 初始化窗口左右指针、窗口长度结果以及当前窗口和
    let left = 0;
    let right = 0;
    let ans = Infinity;
    let sum = 0; 
    
    // S2 模拟像右滑动
    while(right<n){
        // S3 寻找可行解
        sum+=nums[right];
        right++;

        // S4 当已找到可行解时，缩小窗口以优化
        while(sum>=target){
            // S4-1 更新结果值
            ans = Math.min(ans, right-left);
            // S4-2 缩小窗口
            sum-=nums[left];
            left++;
        }
    }

    // 如果 ans 不变，则说明没有符合条件的子数组
    return ans === Infinity ? 0 : ans;
};

leetcode (opens new window)

和至少为 K 的最短子数组 (opens new window)

// 方法一：前缀和 + 单调双端队列 时间复杂度：O(n)
var shortesSubarray = function(nums, k) {
    const n = nums.length;
    const preSumArr = new Array(n + 1).fill(0);
    for(let i = 0; i < n; i++) {
        preSumArr[i + 1] = preSumArr[i] + nums[i]; 
    }
    let res = n + 1;
    const queue = [];
    for(let i = 0; i <= n; i++) {
        const curSum = preSumArr[i];
        while(queue.length !== 0 && curSum - preSumArr[queue[0]] >= k) {
            res = Math.min(res, i - queue.shift());
        }
        while(queue.length !== 0 && preSumArr[queue[queue.length - 1]] >= curSum) {
            queue.pop();
        }
        queue.push(i);
    }
    return res < n + 1 ? res : -1;
}
// 自写---超时 O(n^2)
var shortestSubarray = function(nums, k) {
    const n = nums.length;
    let min = Infinity;
    for(let i = 0; i < n; i ++) {
        let sum = 0;
        for(let j = i; j < n; j ++) {
            sum += nums[j];
            if(sum >= k) {
                min = Math.min(min, j - i + 1);
            }
        }
    }
    return min === Infinity ? -1 : min
};

# [数组]分割数组最大值

定一个非负整数数组 nums 和一个整数 m ，你需要将这个数组分成 m 个非空的连续子数组。

设计一个算法使得这 m 个子数组各自和的最大值最小。

输入：nums = [7,2,5,10,8], m = 2
输出：18
解释：
一共有四种方法将 nums 分割为 2 个子数组。 
其中最好的方式是将其分为 [7,2,5] 和 [10,8] 。
因为此时这两个子数组各自的和的最大值为18，在所有情况中最小。

解答

//贪心算法
var splitArray = function(nums, m) {
    let left = 0; right = 0;
    let len = nums.length;
    for(let i = 0; i < len; i++) {
        right += nums[i];
        if(left < nums[i]) {
            left = num[i];
        }
    }
    function check(mid, m) {
        let sum = 0;
        let cnt = 1;
        for (let i = 0; i < len; i++) {
            if (sum + nums[i] > mid) {
                cnt++;
                sum = nums[i];
            } else {
                sum += nums[i];
            }
        }
        return cnt <= m;
    }
    while(left < right) {
        let mid = Math.floor((left + right) / 2);
        if (check(mid, m)) {
            right = mid;
        } else {
            left = mid + 1;
        }
    }
    return left;
}
// 动态规划
const splitArray = (nums, m) => {
    let len = nums.length;
    let sumList = Array(len + 1).fill(0);
    let dp = Array.from(Array(len + 1), () => Array(m + 1).fill(Infinity));
    // 逐位增加，反面后面根据区间求区间和
    for (let i = 0; i < len; i++) {
        sumList[i + 1] = sumList[i] + nums[i];
      }
    // 默认值
    dp[0][0] = 0;
    for (let i = 1; i <= len; i++) {
        for (let j = 1; j <= Math.min(m, i); j++) {
            // 前i个数分成j段
            for (let x = j - 1; x < i; x++) {
                // x最后一段的起点
                // perv本轮分割完成 分段中最大的和
                let prev = Math.max(dp[x][j - 1], sumList[i] - sumList[x])
                // 该分割情况下最大分段和的最小值
                dp[i][j] = Math.min(prev, dp[i][j])
            }
        }
    }
    return dp[len][m]
}

leetcode (opens new window)

# [数组]长度为k的最大子数组

长度为k的最大子数组的和给定一组大小为n的整数数组，计算长度为k的子数组和的最大值

// 方式一
const add = (array, k) => {
    let index = 0, maxSum = 0;
    for (let i = 0; i < k; i++) {
        maxSum += array[i]
    }
    for (let i = 0; i <= array.length - k; i++) {
        let curSum = 0;
        for (let j = 0; j < k; j++) {
            curSum += array[i + j];
        }
        if (curSum > maxSum) {
            maxSum = curSum;
            index = i;
        }
    }
    return maxSum;
}
// 方式二
const add = (array, k) => {
    let index = 0, maxSum = 0;
    for (let i = 0; i < k; i++) {
        maxSum += array[i];
    }
    let curWindowSum = maxSum;
    for (let i = 1; i <= array.length - k; i++) {
        curWindowSum = curWindowSum - array[i - 1] + array[k + i - 1];
        if (curWindowSum > maxSum) {
            maxSum = curWindowSum;
            index = i;
        }
    }
    return maxSum;
}
console.log(add([1,4,4], 2))

滑动窗口最大值

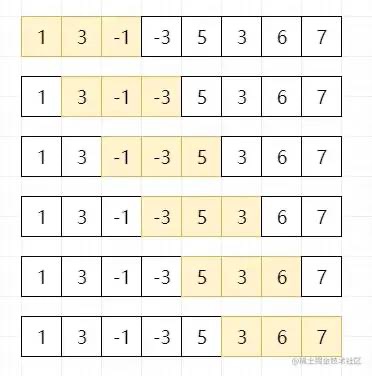
// 题目：给定一个数组 nums，有一个大小为 k 的滑动窗口，从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口中的k个数字。滑动窗口每次只向右移动一位，求返回滑动窗口最大值
// 输入：nums: [1,3,-1,-3,5,3,6,7]；k: 3
// 输出：[3, 3, 5, 5, 6, 7]
const maxSlidingWindow = (nums, k) => {
    // window存储当前窗口中数据的小标
    const window = [];
    // result存储窗口中最大值
    const result = [];
    for(let i = 0; i < nums.length; i++) {
        if(i - window[0] > k - 1) {
            // 剔除窗口长度超出范围时左侧的最大值
            window.shift();
        }
        for(let j = window.length -1; j >= 0; j--) {
            // 当前窗口的值依次和要插入的值做比较，如果小于要插入的值，剔除掉该值，知道window为空位置
            if(nums[window[j]] <= nums[i]) {
                window.pop();
            }
        }
        // 添加右侧新加入的值，插入新值时有两种情况：
        // 1、新值为最大值时，则window此时为空；
        // 2、新值不为最大值时，window已剔除掉比新值小的值
        window.push(i);
        if(i >= k - 1) {
        // 窗口是从0开始移动，当移动的距离大于等于目标范围后，以后再往后移动一次，就要写入当前窗口的最大值
            result.push(nums[window[0]])
        }
    }
    return result;
}

// 第二种
function maxSlidingWindow() {
    let result = [];
    for(let i = 0; i < nums.length - k + 1; i++) {
        result.push(Math.max.apply(null, nums.slice(i, i + k)))
    }
    return result;
}

将x减到0的最小操作数

给你一个整数数组 nums 和一个整数 x 。每一次操作时，你应当移除数组 nums 最左边或最右边的元素，然后从 x 中减去该元素的值。请注意，需要修改数组以供接下来的操作使用。

如果可以将 x 恰好减到 0 ，返回最小操作数；否则，返回 -1 。

// 输入：nums = [3,2,20,1,1,3], x = 10
// 输出：5
// 解释：最佳解决方案是移除后三个元素和前两个元素（总共 5 次操作），将 x 减到 0 。

const minOperations = function(nums, x) {
    let len = nums.length;
    let total = nums.reduce((prev, cur) => prev + cur, 0);
    if(total < x) return -1;
    let ret = Infinity;
    let sum = 0;
    let l = r = 0;
    while(r < len) {
        sum += nums[r];
        while(total - sum < x) {
            // 外面的值已经小于x了，所以需要收缩窗口
            sum -= nums[l];
            l++;
        }
        if(total - sum === x) {
            // 符合要求
            ret = Math.min(ret, len - (r - l + 1));
        }
        r++;
    }
    return ret === Infinity ? -1 : ret;

    // let n = nums.length;
    // let sum = _.sum(nums);
    // if(sum < x) {
    //     return -1;
    // }
    // let right = 0;
    // let lsum = 0;
    // let rsum = sum;
    // let ans = n + 1;
    // for(let left = -1; left < n; left++) {
    //     if(left != -1) {
    //         lsum += nums[left];
    //     }
    //     while(right < n && lsum + rsum > x) {
    //         rsum -= nums[right];
    //         ++right;
    //     }
    //     if(lsum + rsum === x) {
    //         ans = Math.min(ans, (left + 1) + (n - right));
    //     }
    // }
    // return ans > n ? -1 : ans;
}

将x减到0的最小操作数 (opens new window)

# [数组]找到和最大的长度为 K 的子序列

给你一个整数数组 nums 和一个整数 k 。你需要找到 nums 中长度为 k 的子序列，且这个子序列的和最大。

请你返回任意一个长度为 k 的整数子序列。

子序列定义为从一个数组里删除一些元素后，不改变剩下元素的顺序得到的数组。

输入：nums = [2,1,3,3], k = 2
输出：[3,3]
解释：
子序列有最大和：3 + 3 = 6 。

解答

var maxSubsequence = function(nums, k) {
    let num = nums.map((num, index) => ({
        num,
        index,
    })); // 返回对象
    // let num = nums.map((num, index) => {
    //     return {
    //         num,
    //         index
    //     }
    // })
    num = num.sort((x, y) => y.num - x.num).slice(0,k);
    num = num.sort((x, y) => x.index - y.index);
    return num.map((item) => item.num);
};

leetcode (opens new window)

# [数组]-划分为k个相等的子集

给定一个整数数组 nums 和一个正整数 k，找出是否有可能把这个数组分成 k 个非空子集，其总和都相等。

另一提求k的最大值

输入： nums = [4, 3, 2, 3, 5, 2, 1], k = 4
输出： True
说明： 有可能将其分成 4 个子集（5），（1,4），（2,3），（2,3）等于总和。

// 整体思路
// 找子集，相当于找组合，本解法用DFS多叉树来搜索(也可以用DFS二叉树)
// 目标组合需满足和为 target0 = sum(nums) / k;
// 找到目标组合后，继续递归，找到下一个组合
var canPartitionKSubsets = function(nums, k) {
  const total = nums.reduce((total, num) => total + num, 0)
  const target0 = total / k // 目标组合的和
  if (target0 !== Math.floor(target0)) return false
  let used = new Array(nums.length).fill(false)
  nums.sort((a, b) => a - b) // 从小到大排序
  // 如果找到 k - 1 个目标组合，那么剩下的数肯定能组成第 k 个目标组合
  return dfs(target0, k - 1, 0, used, nums)

  // 返回是否找到 k 个目标组合，
  // target 表示当前组合还可以容纳多大的数
  function dfs(target, k, start, used, nums) {
    // 找到一个目标组合，接着找下一个目标组合
    if (target === 0) return dfs(target0, k - 1, 0, used, nums)
    if (k === 0) return true // 已找到所有目标组合
    // 尝试将每个数放入当前组合
    // 因为是找组合，无需回头尝试，比如组合 {a, b} 和组合 {b, a} 是等价的
    for (let i = start; i < nums.length; ++i) {
      if (used[i]) continue
      const num = nums[i]
      // 可行性剪枝: 
      // num 无法构成目标组合
      // nums 从小到大排序，既然 nums[i] 都偏大了， nums[i + 1] 更加偏大，无需尝试
      if (num > target) return false

      used[i] = true
      const got = dfs(target - num, k, i + 1, used, nums) // 找当前组合的下一个数
      if (got) return got
      used[i] = false
    }
    return false
  }
}

划分为k个相等的子集 (opens new window)

划分为k个相等的子集1 (opens new window)

# [数组-回溯]数组组合

力扣地址 (opens new window) 给定两个整数n和k,返回1...n中所有可能的k个数的组合。

示例：

输入: n = 4， k = 2;

输出：
[
    [2,4],
    [3,4],
    [2,3],
    [1,2],
    [1,3],
    [1,4]
]

题解

const combine = function(n, k) {
    const res = [];
    const could = [];
    if (k === 0) {
        return [[]];
    }
    function dfs(start, n, k, res, could) {
        if (could.length === k) {
            res.push(could.slice(0));
            return;
        }
        for (let i = start; i < n + 1; i++) {
            could.push(i);
            dfs(i+1, n, k, res, could);
            could.pop();
        }
        return res;
    }
    return dfs(1, n, k, res, could);
}

数组组合

# [数组-组合]下一个排列

整数数组的一个排列就是将其所有成员以序列或线性顺序排列。

例如，arr = [1,2,3] ，以下这些都可以视作 arr 的排列：[1,2,3]、[1,3,2]、[3,1,2]、[2,3,1] 。

整数数组的下一个排列是指其整数的下一个字典序更大的排列。更正式地，如果数组的所有排列根据其字典顺序从小到大排列在一个容器中，那么数组的下一个排列就是在这个有序容器中排在它后面的那个排列。如果不存在下一个更大的排列，那么这个数组必须重排为字典序最小的排列（即，其元素按升序排列）。

例如，arr = [1,2,3] 的下一个排列是 [1,3,2] 。

类似地，arr = [2,3,1] 的下一个排列是 [3,1,2] 。

而 arr = [3,2,1] 的下一个排列是 [1,2,3] ，因为 [3,2,1] 不存在一个字典序更大的排列。

给你一个整数数组 nums ，找出 nums 的下一个排列。

必须原地修改，只允许使用额外常数空间。

const nextPermutation = nums => {
    for(let i = nums.length - 1; i >= 0; i--) {
        if(nums[i] < nums[i + 1]) {
            const large = nextLarge(i);
            swap(i, large);
            reverse(i + 1);
            return nums;
        }
    }
    nums.reverse();
    return nums;
    function swap(i, j) {
        [nums[i], nums[j]] = [nums[j], nums[i]];
    }
    function reverse(idx) {
        let start = idx, end = nums.length - 1;
        while(start < end) {
            swap(start, end);
            start++;
            end--;
        }
    }
    function nextLarge(idx) {
        for(let i = nums.length - 1; i > idx; i--) {
            if(nums[i] > nums[idx]) return i;
        }
    }
}

# [数组]检查好数组

给你一个正整数数组 nums，你需要从中任选一些子集，然后将子集中每一个数乘以一个任意整数，并求出他们的和。

假如该和结果为 1，那么原数组就是一个「好数组」，则返回 True；否则请返回 False。

// 输入：nums = [12,5,7,23]
// 输出：true
// 解释：挑选数字 5 和 7。
// 5*3 + 7*(-2) = 1
const isGoodArray = function(nums) {
    let divisor = nums[0];
    for(let num of nums) {
        divisor = gcd(divisor, num);
        if(divisor === 1) {
            break;
        }
    }
    return divisor === 1;
}
const gcd = (num1, num2) => {
    while(num2 !== 0) {
        const temp = num1;
        num1 = num2;
        num2 = temp % num2;
    }
    return num1;
}

检查好数组 (opens new window)

# 最长连续序列

给定一个未排序的整数数组 nums ，找出数字连续的最长序列（不要求序列元素在原数组中连续）的长度。

请你设计并实现时间复杂度为 O(n) 的算法解决此问题。

示例 1：

输入：nums = [100,4,200,1,3,2]
输出：4
解释：最长数字连续序列是 [1, 2, 3, 4]。它的长度为 4。

var longestConsecutive = function(nums) {
    //nums未排序，找出数字连续的最长序列，要求O(n)
    let set = new Set(nums);//数组去重放入set中
    let max_len = 0;
    for(let num of set){//遍历集合
        let len =1;
        // 从中心向两边扩散查找
        let left=num-1,right=num+1;
        while(set.has(left)){
            //找到就删掉，避免重复遍历，导致超时
            set.delete(left);
            left--;
            len++;
        }
        while(set.has(right)){
            set.delete(right);
            right++;
            len++;
        }
        max_len = Math.max(len,max_len);
    }
    return max_len;
};

# [动态规划]最长递增子序列

最长递增序列个数给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

输入：nums = [10,9,2,5,3,7,101,18]
输出：4
解释：最长递增子序列是 [2,3,7,101]，因此长度为 4 。

答案

var lengthOfLIS = function(nums) {
    const dp = new Array(nums.length).fill(1);
    for (let i = 0; i < nums.length; i++) {
        // i与i签名的元素比较
        for(let j = 0; j < i;j++) {
            // 找到比i小的元素，找到一个，就让当前的序列的最长序列长度加你
            if(nums[i] > nums[j]) {
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }
    return Math.max(...dp)
}

leetcode (opens new window)

最长递增序列的值

// 题目，一个整数数组的nums, 找出其中一组最长递增子序列的值
// 输入：[3,5,7,1,2,8]
// 输出: [3,5,7, 8]
function lengthOfLIS(nums) {
    if(!nums.length) return 0;
    // 创建一个和原数组等长的数组dp，用来存储每一项的最长递增子序列
    // 比如[1,2,2]，表示第二项和第三项的最长递增子序列都是2
    let dp = new Array(nums.length).fill(1);
    // 双层for循环，每一项都和之前的所有项一一进行比较，计算出该项的最长递增子序列个数，存储到dp中
    for(let i = 0; i < nums.length; i++) {
        for(let j = 0; j < i; j++) {
           if (nums[j] < nums[i]) {
                // 比较当前项已有的最大值和之前项最大值，比如当比较到第三项[1,2,2]时，如第三项比第二项大，所以第三项的计算结果为[1,2,3]
                dp[i] = Math.max(dp[i], dp[j] + 1);
            }
        }
    }
    // 取出一组最长递增子序列的具体值(注意:最长递增子序列有可能有都组值，这里只取出其中一组值)
    let max = Math.max(...dp);
    let result = [];
    for(let i = max; i>= 1; i--) {
        // 倒序遍历，根据长度获取对应的值
        findArrNode(dp, i, result, nums);
    }
    return result;
}
function findArrNode(dp, value, result, arr){
    // 找到符合条件最后一项的下标，这样才能保证数组的顺序是正确的
    let index = dp.lastIndexOf(value);
    // 存储对应的值
    result.push(arr[index]);
    // 对dp进行截取，保证只取到最大项之前的数据
    dp.length = index + 1;
}

# [动态规划]最长递增序列的个数

给定一个未排序的整数数组 nums ，返回最长递增子序列的个数。

注意这个数列必须是严格递增的。

输入: [1,3,5,4,7]
输出: 2
解释: 有两个最长递增子序列，分别是 [1, 3, 4, 7] 和[1, 3, 5, 7]。

解答

const findNumberOfFIS = nums => {
    let n = nums.length, maxLen = 0, ans = 0;
    const dp = new Array(n).fill(0);
    const cnt = new Array(n).fill(0);
    for (let i = 0; i < n; ++i) {
        dp[i] = 1;
        cnt[i] = 1;
        for (let j = 0; j < i; ++j) {
            if (nums[i] > nums[j]) {
                if (dp[j] + 1 > dp[i]) {
                    dp[i] = dp[j] + 1;
                    cnt[i] = cnt[j]; // 重置计数
                } else if (dp[j] + 1 === dp[i]) {
                    cnt[i] += cnt[j];
                }
            }
        }
        if (dp[i] > maxLen) {
            maxLen = dp[i];
            ans = cnt[i]; // 重置计数
        } else if (dp[i] === maxLen) {
            ans += cnt[i];
        }
    }
    return ans;
}

leetcode (opens new window)

# 字符串有效性检查

// '{}[]()'

var isValid = function(s) {
    const stack = [];
    for (let val of s) {
        if('()[]{}'.indexOf(v) < 0) continue
        if (val === '(') stack.push(')');
        else if (val === '[') stack.push(']');
        else if (val === '{') stack.push('}');
        else if (stack.length === 0 || val !== stack.pop()) return false;
    }
    return stack.length === 0;
};

leecode (opens new window)

# 最长有效括号

var longestValidParentheses = function(S) {
    // let maxLen = 0;
    // const stack = [];
    // stack.push(-1);
    // for(let i = 0; i < s.length; i++) {
    //     const c = s[i];
    //     if (c === '(') {
    //         stack.push(i);
    //     } else {
    //         stack.pop();
    //         if (stack.length) {
    //             const curMaxLen = i - stack[stack.length - 1]; // 计算有效连续长度
    //             maxLen = Math.max(maxLen, curMaxLen);          // 挑战最大值
    //         } else {
    //             stack.push(i);
    //         }
    //     }
    // }
    // return maxLen

    let stack = [-1], ans = 0
    for (let i = 0; i < S.length; i++)
        if (S[i] === '(') stack.push(i)
        else if (stack.length === 1) stack[0] = i
        else stack.pop(), ans = Math.max(ans, i - stack[stack.length-1])
    return ans
};

leetcode (opens new window)

真题

# 括号的分数

// 输入： "()()"
// 输出： 2
// 示例 4：

// 输入： "(()(()))"
// 输出： 6
const scoreOfParentheses = s => {
    let stack = [0];
    for(let i = 0; i < s.length; i++) {
        if(s[i] === '(') {
            stack.push(0);
        } else {
            let v = stack.pop();
            let top = stack.pop() + Math.max(2 * v, 1);
            stack.push(top)
        }
    }
    return stack[0]
}

括号的分数 (opens new window)

# 使括号有效的最少添加(贪心)

// 时间复杂度：O(n)O(n)，其中 nn 是字符串的长度。遍历字符串一次。
// 空间复杂度：O(1)O(1)。只需要维护常量的额外空间。
const minAddToMakeValid = s => {
    let ans = 0;
    let leftCount = 0;
    let length = s.length;
    for(let i = 0; i < length; i++) {
        let c = s[i];
        if(c === '(') {
            leftCount++;
        } else {
            if(leftCount > 0) {
                leftCount--;
            } else {
                ans++;
            }
        }
    }
    ans += leftCount;
    return ans;
}
console.log(minAddToMakeValid('())'))

使括号有效的最少添加 (opens new window)

# 会议室问题

会议室① 给定一个会议时间安排的数组intervals，每个会议时间都会包括开始和结束时间intervals[i] = [starti, endi],请你判断一个人是否能够参加里面的全部会议示例

输入:intervals = [[0, 30], [5, 10], [15, 20]]
输出false

解题：

/**
 * 方法一暴力法
 * 最简单的方法是将数组中的会议室量量比较，判断他们是否冲突(即他们之间是否有交叠)，如果一个会议室开的时候，另一个依然没有结束，则他们存在交叠，就没法同时参加
*/
var canAttendMeetings = function(intervals) {
  for(let i = 0; i < intervals.length; i++) {
    for (let j = i + 1; j < intervals.length; j++) {
      if (overlap(intervals[i], intervals[j])) {
        return false;
      }
    }
  }
  return true;
}
function overlap(nums1, nums2) {
  return ((nums1[0] >= nums2[0] && nums1[0] < nums2[1]) || (nums2[0] >= nums1[0] && nums2[0] < nums1[1]))
}
// 方法二排序
// 思路是按照开始时间进行排序，接着一次遍历会议，检查它是否在下一个会议的开始前结束
var canAttendMeetings = function(intervals) {
  // 将传入的数组按照 第一个数字升序排列
  intervals.sort((a, b) => b[0] - a[0]);

  for (let i = 0; i < intervals.length; i++) {
    if (intervals[i][1] > intervals[i + 1][0]) {
      return false;
    }
  }
  return true;
}

会议室② 给定一个会议时间安排的数组，每个会议时间都会包括开始和结束的时间 [[ s1 , e1 ] ，[ s2 , e2 ]，…] (si < ei) ，为避免会议冲突，同时要考虑充分利用会议室资源，请你计算至少需要多少间会议室，才能满足这些会议安排。例如:

输入: [[0, 30],[5, 10],[15, 20]]

输出: 2

面试现场讨论了算法原理，未有时间编码调试：

function fn(arr) {
    const sortArr = arr.sort((a,b) => a[0] - b[0]);
    console.log(sortArr);
    let number = 1;
    let end = sortArr[0][1];
    for (let i = 1; i < sortArr.length; i++) {
        if (sortArr[i][0] < end) {
            end !== sortArr[i][0] ? number++ : '';
        }
        end = sortArr[i][1];
    }
    return number;
}
console.log(fn([[0, 30],[5, 10],[15, 20], [10,35], [20, 30]]));

解题思路
[u, v] 代表一个人在 u 时刻上车， v 时刻下车

把上下车的事件全部排序，同时先下后上。

求在车上的最大人数。

var minMeetingRooms = function(intervals) {
    let nums = [];

    //转换为上下车问题
    for (let [u, v] of intervals){
        nums.push([u, 1]);
        nums.push([v, -1]);
    }
    nums.sort((a, b) => a[0] == b[0] ? a[1] - b[1] : a[0] - b[0]);

    let ans = 0, cur = 0;
    for (let [time, e] of nums){
        cur += e;
        ans = Math.max(cur, ans);
    }
    return ans;
};

# 加油站

leetcode (opens new window)

输入: 
gas  = [1,2,3,4,5]
cost = [3,4,5,1,2]

输出: 3

解释:
从 3 号加油站(索引为 3 处)出发，可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
开往 4 号加油站，此时油箱有 4 - 1 + 5 = 8 升汽油
开往 0 号加油站，此时油箱有 8 - 2 + 1 = 7 升汽油
开往 1 号加油站，此时油箱有 7 - 3 + 2 = 6 升汽油
开往 2 号加油站，此时油箱有 6 - 4 + 3 = 5 升汽油
开往 3 号加油站，你需要消耗 5 升汽油，正好足够你返回到 3 号加油站。
因此，3 可为起始索引。

var canCompleteCircuit = function(gas, cost) {
    let curSum = 0, // 当前站点的剩余油料
        start = 0,
        totalSum = 0; // 总的剩余油料

    for(let i = 0; i < cost.length; i++) {
        curSum += gas[i] - cost[i];
        if(curSum < 0) {
            start = i+1;
            curSum = 0;
        }
        totalSum += gas[i] - cost[i];
    }

    return start >= gas.length || totalSum < 0  ? -1 : start;
};

# 山脉数组的峰顶索引

// 方法一:枚举
var peakIndexInMountainArray = function(arr) {
    const n = arr.length;
    let ans = -1;

    for (let i = 1; i < n - 1; ++i) {
        if (arr[i] > arr[i + 1]) {
            ans = i;
            break;
        }
    }
    return ans;
};

// 二分查找
var peakIndexInMountainArray = function(arr) {
    const n = arr.length;
    let left = 1, right = n - 2, ans = 0;
    while(left <= right) {
        const mid = Math.floor((left + right) / 2);
        if (arr[mid] > arr[mid + 1]) {
            ans = mid;
            right = mid - 1;
        } else {
            left = mid + 1;
        }
    }
    return ans;
}

leecode (opens new window)

# 山脉数组中查找目标值

输入：array = [1,2,3,4,5,3,1], target = 3

输出：2

解释：3 在数组中出现了两次，下标分别为 2 和 5，我们返回最小的下标 2。

var findInMountainArray = function(target, mountainArr) {
    let l = 0, r = mountainArr.length() - 1
    
    // 二分求 峰顶
    while (l < r) {
        let mid = Math.floor((l + r) / 2)
        
        if (mountainArr.get(mid) > mountainArr.get(mid + 1)) {
            r = mid
        } else {
            l = mid + 1
        }
    }
        
    let peak = r;

    // 搜索左边
    let index = binary_search(mountainArr, target, 0, peak, x => x)
    
    // 如果目标在左边, 返回
    if (index !== -1) return index
    
    // 如果目标不在左边, 搜索右边
    return binary_search(mountainArr, target, peak + 1, mountainArr.length() - 1, x => -x)
};

function binary_search(mountain, target, l, r, callback) { // callback 方法处理递增还是递减
    
    target = callback(target)

    while (l <= r) {
        let mid = Math.floor((l + r) / 2)
        let midValue = callback(mountain.get(mid))
        
        if (midValue === target) {
            return mid
        } else if (midValue < target) {
            l = mid + 1
        } else {
            r = mid - 1
        }  
    } 
    return -1
}

# 螺旋矩阵

给你一个m行n列的矩阵matrix，请按照顺时针螺旋顺序，返回矩阵中所有元素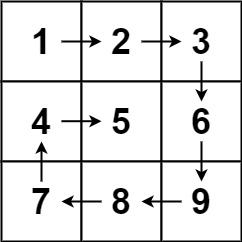螺旋矩阵0 输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]

输出：[1,2,3,6,9,8,7,4,5]

螺旋矩阵

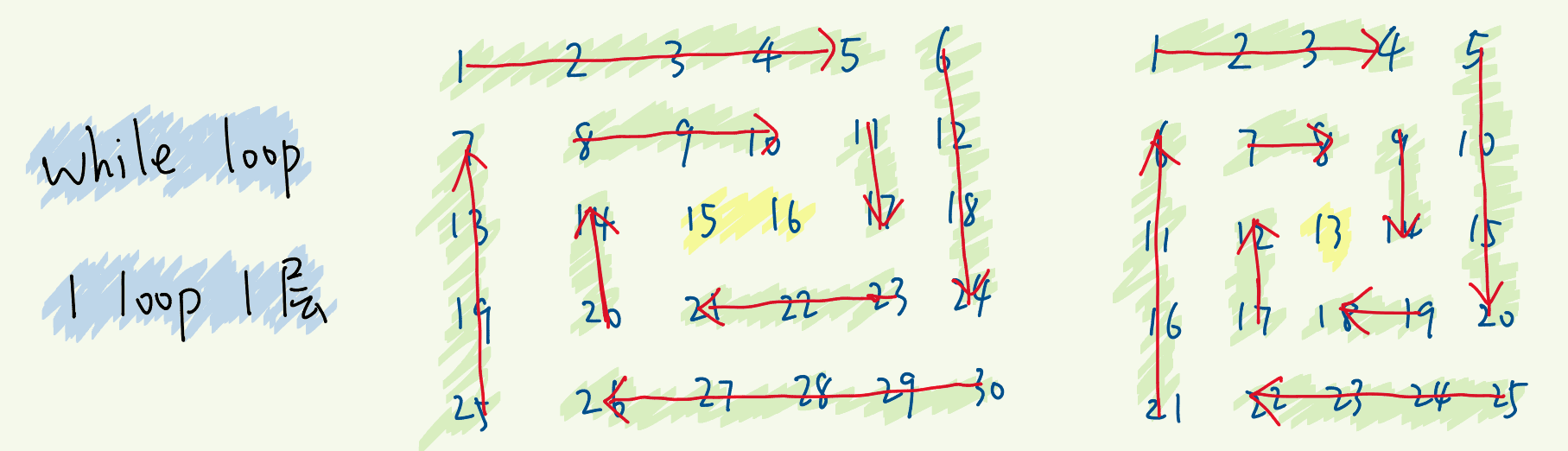
如果一条边从头遍历到底，则下一条边遍历的起点随之变化
如果不遍历到底，可以减小横向、竖向遍历之间的影响
一轮迭代结束时，4条边的两端同事收窄1
一轮迭代所有的事情变得很清晰：遍历一个圈，遍历的返回收缩为内圈
不再形成环了，就会剩下下一行或一列，然后单独判断

var spiralOrder = function(matrix) {
    if(matrix.length === 0) return [];
    const res = [];
    let top = 0;
    let bottom = matrix.length - 1;
    let left = 0;
    let right = matrix[0].length - 1;
    while(top < bottom && left < right) {
        for (let i = left; i < right; i++) res.push(matrix[top][i]); // 上层
        for (let i = top; i < bottom; i++) res.push(matrix[i][right]); // 右层
        for (let i = right; i > left; i--) res.push(matrix[bottom][i]); // 下层
        for (let i = bottom; i > top; i--) res.push(matrix[i][left]); // 左层
        right--;
        top++;
        left++;
        bottom--; // 四个边界同事收缩，进入内层
    }
    if(top === bottom) { // 剩下一行，从左到右依次添加
        for (left i = left; i <= right; i++) res.push(matrix[top][i]);
    } else if(left === right) { // 剩下一列，从上到下依次添加
        for (let i = top; i <= bottom; i++) res.push(matrix[i][left]);
    }
    return res;
}

螺旋数组 (opens new window)

螺旋矩阵

# LRU 缓存机制

问题

输入
["LRUCache", "put", "put", "get", "put", "get", "put", "get", "get", "get"]
[[2], [1, 1], [2, 2], [1], [3, 3], [2], [4, 4], [1], [3], [4]]
输出
[null, null, null, 1, null, -1, null, -1, 3, 4]

答题

var LRUCache = function(capacity) {
    this.map = new Map();
    this.capacity = capacity;
}

LRUCache.prototype.get = function(key) {
    if (this.map.has(key)) {
        var temp = this.map.get(key);
        this.map.delete(key);
        this.map.set(key, temp);
        return temp
    } else {
        return -1
    }
}

LRUCache.prototype.put = function(key, value) {
    if(this.map.has(key)) {
        this.map.delete(key);
    }
    this.map.set(key, value);
    if(this.map.size > this.capacity) {
        this.map.delete(this.map.keys().next().value);
    }
}

力扣 (opens new window)

LRUCatch空间复杂度 (opens new window)

扩展

var arr = [1,2,3,4,5]
arr.keys().next(); // {value: 0, done: false}

arr.keys() // Array Iterator {}

# [贪心]超级洗衣机

假设有 n 台超级洗衣机放在同一排上。开始的时候，每台洗衣机内可能有一定量的衣服，也可能是空的。

在每一步操作中，你可以选择任意 m (1 <= m <= n) 台洗衣机，与此同时将每台洗衣机的一件衣服送到相邻的一台洗衣机。

给定一个整数数组 machines 代表从左至右每台洗衣机中的衣物数量，请给出能让所有洗衣机中剩下的衣物的数量相等的最少的操作步数。如果不能使每台洗衣机中衣物的数量相等，则返回 -1 。

示例 1：

输入：machines = [1,0,5]

输出：3

解释：

第一步: 1 0 <-- 5 => 1 1 4

第二步: 1 <-- 1 <-- 4 => 2 1 3

第三步: 2 1 <-- 3 => 2 2 2

var findMinMoves = function(machines) {
    const tot = eval(machines.join('+'));
    const n = machines.length;
    if (tot % n !== 0) {
        return -1;
    }
    let avg = Math.floor(tot / n);
    let ans = 0, sum = 0;
    for (let num of machines) {
        num -= avg;
        sum += num;
        ans = Math.max(ans, Math.max(Math.abs(sum), num));
    }
    return ans;
}

力扣地址 (opens new window)

# [动态规划]编辑距离

给你两个单词word1和word2,请你计算出将word1转换成word2所使用的最少操作数

你可以对一个单词进行如下三种操作

插入一个字符
删除一个字符
替换一个字符

实例

示例 1：

输入：word1 = "horse", word2 = "ros"
输出：3
解释：
horse -> rorse (将 'h' 替换为 'r')
rorse -> rose (删除 'r')
rose -> ros (删除 'e')

示例 2：
输入：word1 = "intention", word2 = "execution"
输出：5
解释：
intention -> inention (删除 't')
inention -> enention (将 'i' 替换为 'e')
enention -> exention (将 'n' 替换为 'x')
exention -> exection (将 'n' 替换为 'c')
exection -> execution (插入 'u')

编写

// 暴力解-- 容易理解
var minDistance = function(word1, word2) {
    const dp = (i, j) => {
        // 因为递归传入的是上一次(i - 1, j -1 )所以这里都需要 + 1;
        if (i === -1) return j + 1; // s1走完了，将s2剩下的插入s1，需要j + 1步
        if (j === -1) return i + 1; // s2走完了，删除s1剩下的，需要i+ 1步
        if(word1[i] === word2[j]) {
            return dp(i - 1, j - 1); // 什么都不做，i,j向前移一位
        } else {
            // 找出最小的
            return Math.min(
                dp(i, j - 1) + 1, // 插入，在word1中插入word2[j]一样的字符，相当于把word2向前移动1位，word1不动
                dp(i - 1, j) + 1, // 删除，把word1[i]删除，相当于word1向前移动1位，word2不动
                dp(i - 1, j - 1) + 1 // 替换操作，都向前移动1位
            )
        }
    }
    // 从后往前遍历，i， j 初始化指向最后一个索引
    return dp(word1.length - 1, word2.length - 1)
}
// 动态规划
function minDistance(word1, word2) {
    const m = word1.length, n = word2.length;
    // 我们要多添加一行一列，用来做base case
    const dp = Array.from(Array(word1.length + 1), () => Array(word2.length+1).fill(0));
    // 添加一列，base case
    for (let i = 1; i <= m; i++) {
        dp[i][0] = i;
    }
    // 添加一行，base case
    for (let i = 1; i <= n; i++) {
        dp[0][i] = i;
    }
    // 因为我们补了一行/列base case,这里都从1开始
    for (let i = 1; i <= m; i++) {
        for (let j = 1; j <= n; j++) {
            if (word1[i - 1] === word2[j - 1]) { // 相等，什么都不做
                dp[i][j] = dp[i - 1][j - 1]
            } else {
                dp[i][j] = Math.min(
                    dp[i - 1][j] + 1, // s1删除操作
                    dp[i][j - 1] + 1, // s1插入操作
                    dp[i -1][j - 1] + 1 // 替换
                )
            }
        }
    }
    return dp[m][n]
}

参考 (opens new window)

# 单词接龙

字典 wordList 中从单词 beginWord 和 endWord 的转换序列是一个按下述规格形成的序列 beginWord -> s1 -> s2 -> ... -> sk：

每一对相邻的单词只差一个字母。对于 1 <= i <= k 时，每个 si 都在 wordList 中。注意， beginWord 不需要在 wordList 中。 sk == endWord 给你两个单词 beginWord 和 endWord 和一个字典 wordList ，返回从 beginWord 到 endWord 的最短转换序列中的单词数目。如果不存在这样的转换序列，返回 0 。

输入：beginWord = "hit", endWord = "cog", wordList = ["hot","dot","dog","lot","log","cog"]
输出：5
解释：一个最短转换序列是 "hit" -> "hot" -> "dot" -> "dog" -> "cog", 返回它的长度 5。

const ladderLength = (beginWord, endWord, wordList) => {
    const wordSet = new Set(wordList);
    const queue = [];
    queue.push([beginWord, 1]);
    while(queue.length) {
        const [word, level] = queue.shift(); // 当前出列的单词
        if(word === endWord) {
            return level
        }
        for (let i = 0; i < word.length; i++) { // 遍历当前单词的所有字符
            for(let c = 97; c <= 122; c++) { // 对应26个字母
                const newWord = word.slice(0, i) + String.fromCharCode(c) + word.slice(i + 1); // 形成新词
                if (wordSet.has(newWord)) { // 单词表里有这个新词
                    queue.push([newWord, level + 1]); // 作为下一层的词入列
                    wordSet.delete(newWord);  // 避免该词重复入列
                }
            }
        }
    }
    return 0; // bfs结束 始终没有遇到终点
}

leetcode (opens new window)

# 所有子字符串美丽值之和

一个字符串的美丽值定义为:出现频率最高字符与出现频率最低字符的出现次数之差。

比方说, 'abaacc'的美丽值为3-1 = 2；给你一个字符串s,请你放回它所有字符串的美丽值之和

示例1

输入：s = "aabcb"
输出：5
解释：美丽值不为零的字符串包括 ["aab","aabc","aabcb","abcb","bcb"] ，每一个字符串的美丽值都为 1 。

求解

/**
 * 暴力解
*/
var beautySum = function(s) {
  let ret = 0;
  for (let i = 1; i <= s.length; i++) {
    for (let j = 0; j < i; j++) {
      let tmp = s.slice(j, i);
      let map = {}

      let min = Infinity;
      let max = -Infinity;
      for(let i = 0; i < tmp.length; i++) {
        map[tmp[i]] = map[tmp[i]] || 0;
        map[tmp[i]]++;
      }
      for (let item in map) {
        min = Math.min(min, map[item]);
        max = Math.max(max, map[item]);
      }
      ret += (max - min)
    }
  }
  return ret;
}

// 解题思路
// 双循环的思路最简单，直接里外两层循环 排列组合所有可能的子字符串，然后统计他们出现的次数，最大值 - 最小值 累积。

// 这里用了一个小技巧：使用数组来记录出现的次数。这样做的原因是，通过 fromCharCode() 方法转换，得到字符和数字之间的关系，也推导得到统计数组的下标关系。
var beautySum = function(s) {
  const len = s.length
  if (len < 3) { return 0 }

  const map = {}
  for (let i = 0; i < 26; i++) {
    map[String.fromCharCode(97 + i)] = i
  }

  let i = 0, j = 0
  let min = 0, sum = 0
  let countArr = []
  while (i < len) {
    j = i + 2
    countArr = (new Array(26)).fill(0)
    countArr[map[s[i]]] += 1
    countArr[map[s[i + 1]]] += 1
    while (j < len) {
      countArr[map[s[j]]] += 1
      min = Math.min(...(countArr.filter(i => i > 0)))
      if (isFinite(min)) {
        sum = sum + Math.max(...countArr) - min
      }

      j++
    }

    i++
  }

  return sum
};

leetcode (opens new window)

# N皇后

n皇后问题研究的是如何将n个换后放置在n * n的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数n,返回所有不同的n皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

N皇后

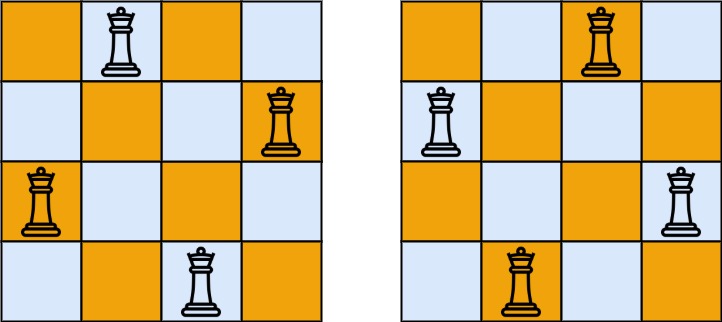
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

const solveQueens = n => {
    const board = Array.from(Array(n), ()=> Array(n).fill('.')); // 棋盘初始化
    const res = [];
    const isValid = (row, col) => {
        for (let i = 0; i < row; i++) { // 之前的行
            for(let j = 0; j < n; j++) { // 所有的列
                if(board[i][j] === 'Q' && 
                    (j === col || i + j === row + col || i - j === row - col)) { //发现了皇后 并且和自己同列/对角线
                    return false; // 不是合法选择
                }
            }
        }
        return true;
    }
    const helper = row => { // 放置当前行的皇后
        if(row === n) { // 递归的出口，超出了最后一行
            const stringsBoard = board.slice(); // 拷贝一份board
            for(let i = 0; i < n; i++) {
                stringsBoard[i] = stringsBoard[i].join(''); // 将每一行拼成字符串
            }
            res.push(stringsBoard); // 推入res数组
            return;
        }
        for(let col = 0; col < n; col++) { // 枚举出所有选择
            if(isValid(row, col)) { // 剪掉无效的选择
                board[row][col] = 'Q'; // 做出选择，放置皇后
                helper(row + 1); // 继续选择，往下递归
                board[row][col] = '.'; // 撤销当前选择
            }
        }
    }
    helper(0); // 从第0行开始放置
    return res;
}

leetcode (opens new window)

# 矩形重叠

矩形以列表 [x1, y1, x2, y2] 的形式表示，其中 (x1, y1) 为左下角的坐标，(x2, y2) 是右上角的坐标。矩形的上下边平行于 x 轴，左右边平行于 y 轴。

如果相交的面积为正，则称两矩形重叠。需要明确的是，只在角或边接触的两个矩形不构成重叠。

给出两个矩形 rec1 和 rec2 。如果它们重叠，返回 true；否则，返回 false 。

示例 1：

输入：rec1 = [0,0,2,2], rec2 = [1,1,3,3]
输出：true

矩形重叠

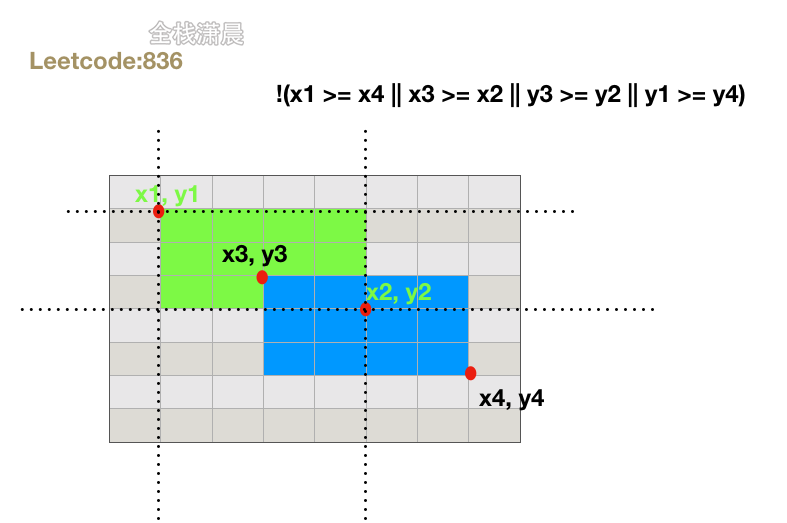
const isRectangleOverlap = (rec1, rec2) => {
    const [x1, y1, x2, y2] = rec1;
    const [x3, y3, x4, y4] = rec2;
    return !(x1 >= x4 || x3 >= x2 || y3 >= y2 || y1 >= y4);
}

# 矩形面积

给你二维平面上两个由直线构成且边与坐标轴平行/垂直的矩形，请你计算并返回两个矩形覆盖的总面积。

每个矩形由其左下顶点和右上顶点坐标表示：

第一个矩形由其左下顶点 (ax1, ay1) 和右上顶点 (ax2, ay2) 定义。第二个矩形由其左下顶点 (bx1, by1) 和右上顶点 (bx2, by2) 定义。

示例 1：

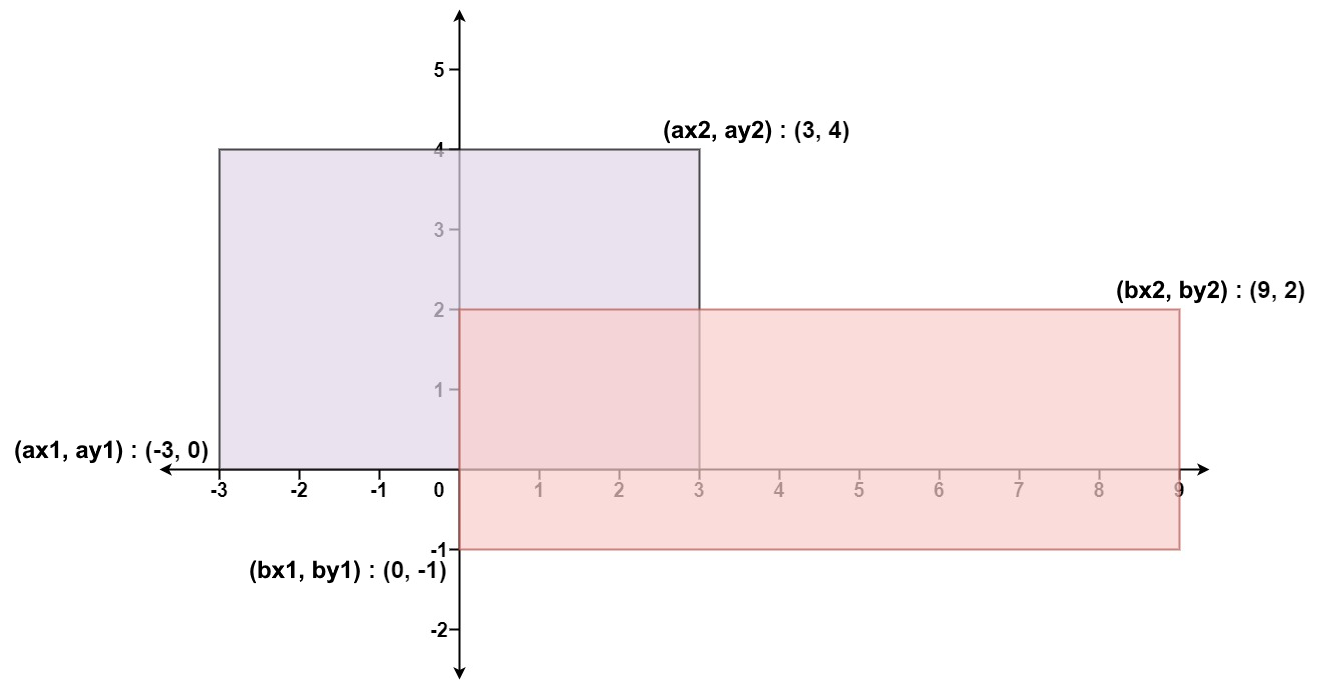
输入：ax1 = -3, ay1 = 0, ax2 = 3, ay2 = 4, bx1 = 0, by1 = -1, bx2 = 9, by2 = 2
输出：45

解题：两个矩形覆盖的总面积等于两个矩形的面积之和减去两个矩形的重叠部分的面积。由于两个矩形的左下顶点和右上顶点已知，因此两个矩形的面积可以直接计算。如果两个矩形重叠，则两个矩形的重叠部分也是矩形，重叠部分的面积可以根据重叠部分的边界计算。

const computeArea = (ax1, ay1, ax2, ay2, bx1, by1, bx2, by2) => {
    const area1 = (ax2 - ax1) * (ay2 - ay1), area2 = (bx2 - bx1) * (by2 - by1);
    const overlapWidth = Math.min(ax2, bx2) - Math.max(ax1, bx1);
    const overlapHeight = Math.min(ay2, by2) - Math.max(ay1, by1);
    const overlapArea = Math.max(overlapWidth, 0) * Math.max(overlapHeight, 0);
    return area1 + area2 - overlapArea;
}

leetCode (opens new window)

# 最小面积矩形

给定在xy平面上的一组点，确定由这些点组成的矩形的最小面试，其中矩形的边平行于x轴和Y轴，如果没有返回任何矩形，就返回0

输入：[[1,1],[1,3],[3,1],[3,3],[2,2]]
输出：4

解答

// 1.先对点集按x后y,值从小到大排序；
// 2. 暴力枚举矩形的左下、右上点，查看是否存在对应的左上、右下点即可
var minAreaRect = function(points) {
    // 1.map
    // 左下，右上枚举
    points.sort((a, b) => a[0] - b[0]);
    let m = new Map();
    let res = Infinity;
    for (let [x, y] of points) {
        if (!m.has(x)) m.set(x, new Set());
        m.get(x).add(y);
    }
    for (let i = 0; i < points.length - 1; i++) {
        for (j = i + 1; j < points.length; j++) {
            let [x1, y1] = points[i];
            let [x2, y2] = points[j];
            if (x1 < x2 && y1 < y2) {
                if (m.get(x1).has(y2) && m.get(x2).has(y1)) {
                    res = Math.min(res, (x2 - x1) * (y2 - y1))
                }
            }
        }
    }
    return res === Infinity ? 0 : res;
}

# 柱状图中最大的矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

// 输入：heights = [2,1,5,6,2,3]
// 输出：10
// 解释：最大的矩形为图中红色区域，面积为 10

const largestRectangleArea = heights => {
    let maxArea = 0
    const stack = [] //单调递增栈 注意栈存的时下标
    heights = [0, ...heights, 0]    //在heights数组前后增加两个哨兵 用来清零单调递增栈里的元素   
    for (let i = 0; i < heights.length; i++) {
        //当前元素对应的高度小于栈顶元素对应的高度时
        while (heights[i] < heights[stack[stack.length - 1]]) {
            const stackTopIndex = stack.pop() //出栈
            maxArea = Math.max(               //计算面积 并更新最大面积
                maxArea,
                heights[stackTopIndex] * (i - stack[stack.length - 1] - 1)//高乘宽
            )
        }
        stack.push(i)//当前下标加入栈
    }
    return maxArea
}

柱状图中最大的矩形 (opens new window)

# 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]

// dfs
const numIslands = (grid) => {
    let count = 0
    for (let i = 0; i < grid.length; i++) {
        for (let j = 0; j < grid[0].length; j++) {
            if (grid[i][j] === '1') {
                count++
                turnZero(i, j, grid)
            }
        }
    }
    return count
}
function turnZero(i, j, grid) {
    if (i < 0 || i >= grid.length || j < 0 || j >= grid[0].length || grid[i][j] === '0') return
    grid[i][j] = '0'
    turnZero(i, j + 1, grid)
    turnZero(i, j - 1, grid)
    turnZero(i + 1, j, grid)
    turnZero(i - 1, j, grid)
}

leetcode (opens new window)

岛屿面积 (opens new window)

const maxAreaOfIsland = grid => {
    const n = grid.length;
    const m = grid[0].length;
    let res = 0;
    // 将每一个岛屿看成图的每一个节点
    // 记录每一个节点的颜色：1未访问 0 被访问过了
    let colors = new Array(n).fill(0).map(() => new Array(m).fill(1));
    for (let i = 0; i < n; i++) {
        for (let j = 0; j < m; j++) {
            if (grid[i][j] == 1) {
                let result = dfs(i, j);
                result > res && res = result;
            }
        }
    }
    return res;
}
// dfs
function dfs(i, j) {
    if (i < 0 || j >=n || j < 0 || j >=m) return 0;
    let result = 0;
    const num = grid[i][j];
    const color = colors[i][j];
    colors[i][j] = 0;
    if (num && color) {
        result += dfs(i + 1, j);
        result += dfs(i - 1, j);
        result += dfs(i, j - 1);
        result += dfs(i, j + 1);
        result++;
    }
    return result;
}

# 种花

假设有一个很长的花坛，一部分地块种植了花，另一部分却没有。可是，花不能种植在相邻的地块上，它们会争夺水源，两者都会死去。

给你一个整数数组 flowerbed 表示花坛，由若干 0 和 1 组成，其中 0 表示没种植花，1 表示种植了花。另有一个数 n ，能否在不打破种植规则的情况下种入 n 朵花？能则返回 true ，不能则返回 false。

输入：flowerbed = [1,0,0,0,1], n = 1
输出：true

const canPlaceFlwers = (flowerbed, n) => {
    let count = 0;
    for (let i = 0, length = flowerbed.length;i < length; i++) {
        // 当前位置是0， 并且前后都不是1，考虑在最前和最后的情况
        if(flowerbed[i] === 0 && flowerbed[i - 1] !=== 1 && flowerbed[i + 1] !== 1) {
            count++;
            i++
        }
    }
    return count >= n;
}

leetcode (opens new window)

# 鸡蛋掉落

示例 1：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。 
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。 
如果它没碎，那么肯定能得出 f = 2 。 
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

解答

// 递归
var superEggDrop = function(k, n) {
    const memo = new Map();
    function dp (k, n) {
        if (k === 1) return n; // 当k为1时，只能线性扫描所有楼层
        if (n === 0) return 0;
        if (memo.has(k + '' + n)) {
            return memo.get(k + '' + n)
        }
        let res = Infinity;
        for (let i = 1; i <= n; i++) {
            res = Math.min(
                res,
                Math.max(
                    dp(k, n - i),
                    dp(k - 1, i - 1)
                ) + 1
            )
        }
        memo.set(k + '' + n, res)
        return res;
    }
    return dp(k, n)
};
// 动态规划
var superEggDrop = function (k, n) {
  // 不选择dp[k][M]的原因是dp[M][k]可以简化操作
  const dp = Array(n + 1).fill(0).map((_) => Array(k + 1).fill(0));

  let m = 0;
  while (dp[m][k] < n) {
    m++;
    for (let j = 1; j <= k; ++j) dp[m][j] = dp[m - 1][j - 1] + 1 + dp[m - 1][j];
  }
  return m;
};

leetcode (opens new window)

# [拓扑]课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。

例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

输入：numCourses = 2, prerequisites = [[1,0]]
输出：true
解释：总共有 2 门课程。学习课程 1 之前，你需要完成课程 0 。这是可能的。
示例 2：

输入：numCourses = 2, prerequisites = [[1,0],[0,1]]
输出：false
解释：总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0 ；并且学习课程 0 之前，你还应先完成课程 1 。这是不可能的。

[[1,0]] 类似 {srouce: 0, target: 1}

const canFinish = (numCourses, prerequisites) => {
    const inDegree = new Array(numCourses).fill(0); // 入度数组
    const map = {}; // 邻接表
    for(let i = 0; i < prerequisites.length; i++) {
        inDegree[prerequisites[i][0]]++; // 求课的初始入度值
        if(map[prerequisites[i][1]]) { // 当前课已经存在于邻接表
            map[prerequisites[i][1]].push(prerequisites[i][0]); // 添加依赖它的后续课
        } else { // 当前可不存在邻接表
            map[prerequisites[i][1]] = [prerequisites[i][0]]
        }
    }
    const queue = [];
    for (let i = 0; i < inDegree.length; i++) { // 所有入度为0的课入列
    if (inDegree[i] == 0) queue.push(i);
  }
  let count = 0;
  while (queue.length) {
    const selected = queue.shift();           // 当前选的课，出列
    count++;                                  // 选课数+1
    const toEnQueue = map[selected];          // 获取这门课对应的后续课
    if (toEnQueue && toEnQueue.length) {      // 确实有后续课
      for (let i = 0; i < toEnQueue.length; i++) {
        inDegree[toEnQueue[i]]--;             // 依赖它的后续课的入度-1
        if (inDegree[toEnQueue[i]] == 0) {    // 如果因此减为0，入列
          queue.push(toEnQueue[i]);
        }
      }
    }
  }
  return count == numCourses; // 选了的课等于总课数，true，否则false
}

leetcode (opens new window)

JS实现判断DAG图是否有环

# 自除数

自除数是指可以被它包含的每一位数整除的数。

例如，128 是一个自除数，因为 128 % 1 == 0，128 % 2 == 0，128 % 8 == 0。自除数不允许包含 0 。

给定两个整数 left 和 right ，返回一个列表，列表的元素是范围 [left, right] 内所有的自除数。

const selfDividingNumber = (left, right) => {
    const res = [];
    for (let i = left; i < right; i++) {
        if (isSelfDividing(i)) {
            res.push(i)
        }
    }
    return res;
}
const isSelfDividing = num => {
    let temp = num;
    while(temp > 0) {
        const digit = temp % 10;
        if (digit === 0 || num % digit !=== 0) {
            return false;
        }
        temp = Math.floor(temp / 10);
    }
    return true;
}

leetcode (opens new window)

# 水仙花数

如果一个三位数，它每个位上的数字的 3 次幂之和等于它本身，那么这个数就是一个水仙花数。

水仙花数是自幂数中的一种，自幂数是指一个 n 位数，它的每个位上的数字的 n 次幂之和等于它本身

当这个 n=3 的时候，这个自幂数也被称为水仙花数

与水仙花数类似的还有四叶玫瑰数(n=4)、五角星数(n=5)等等

// 判断是否
function isSelfPower(num) {
    // 将数字转为字符串
    const n = num.toString();
    const len = n.length;
    const sum = n.split('').reduce((res, i) => {
        // 累加没位数的len次幂
        return res + Math.pow(i, len); // res + i ** len
    }, 0)
    return `${sum}` === `${num}`;
}
(function() {
    const arr = [];
    for (let i = 100; i < 1000; i++) {
        isSelfPower(i) && arr.push(i);
    }
    console.log('水仙花数有:', arr)
})()

// 另一个 十位数n的包含的水仙花数
function flownumber(n) {
    const digits = Array.from({length: 10}, (_, i) => i ** n);

    function isFlower(num) {
        return [...String(num)].reduce((a, b) =>  a + digits[+b], 0) === num; // 例如：i ** len 3**10
    }

    let result = [];
    let start = 10 ** n;
    let end = 10 ** (n + 1) - 1;
    for (let i = start; i <= end; i++) {
        if (isFlower(i)) {
            result.push(i);
        }
    }
    return result;
}

# 使绳子变成彩色的最短时间

单指针形式

leetcode (opens new window)

// 输入：colors = "abaac", neededTime = [1,2,3,4,5]
// 输出：3
// 解释：在上图中，'a' 是蓝色，'b' 是红色且 'c' 是绿色。
// Bob 可以移除下标 2 的蓝色气球。这将花费 3 秒。
// 移除后，不存在两个连续的气球涂着相同的颜色。总时间 = 3 。

const minCost = function(colors, neededTime) {
    // 记录连续的相同颜色气球序列中:加和、最大值
    let res = 0;
    let c = 0;
    while(c < colors.length) {
        let cur = 0;
        let curColor = colors[c];
        let max = 0;
        while(c < colors.length && colors[c] === curColor) {
            cur += neededTime[c]; // 满足条件 相加的值
            max = Math.max(max, neededTime[c]); // 找到大的那个值
            c += 1;
        }
        res += cur - max; // 满足条件相加的值 减去大的值 得到用时较少的那个 累加
    }
    return res;
}

相邻且相等，则消除

# [滑动窗口]学生分数的最小差值

// 输入：nums = [9,4,1,7], k = 2
// 输出：2
// 解释：选出 2 名学生的分数，有 6 种方法：
// - [9,4,1,7] 最高分和最低分之间的差值是 9 - 4 = 5
// - [9,4,1,7] 最高分和最低分之间的差值是 9 - 1 = 8
// - [9,4,1,7] 最高分和最低分之间的差值是 9 - 7 = 2
// - [9,4,1,7] 最高分和最低分之间的差值是 4 - 1 = 3
// - [9,4,1,7] 最高分和最低分之间的差值是 7 - 4 = 3
// - [9,4,1,7] 最高分和最低分之间的差值是 7 - 1 = 6
// 可能的最小差值是 2

const minimumDifference = (nums, k) => {
    if(k === 1) return 0;
    nums.sort((a, b) => a - b);
    let ans = Infinity;
    for(let i = 0; i <= nums.length - k; i++) {
        ans = Math.min(ans, nums[i + k - 1] - nums[i]);
    }
    return ans;
}

# 基本计算器

给你一个字符串表达式s，请你实现一个基本计算器来计算并返回它的值。

// 输入： s = '1 + 1';
// 输出2

// 输入：s = "(1+(4+5+2)-3)+(6+8)"
// 输出：23
const calculate = s => {
    let ans = 0;
    let num_stack = [];
    let op_stack = [];
    let sign = 1;
    for (let i = 0; i < s.length; i++) {
        if (s[i] == ' ') continue;
        if (s[i] == '+' || s[i] == '-') sign = s[i] == '+' ? 1 : -1;
        else if (s[i] >= '0' && s[i] <= '9') {
            let num = parseInt(s[i]);
            while (i < s.length - 1 && s[i + 1] >= '0' && s[i + 1] <= '9') {
                num = num * 10 + parseInt(s[++i]);
            }
            ans += sign * num;
        } else if (s[i] == '(') {
            num_stack.push(ans);
            op_stack.push(sign);
            ans = 0;
            sign = 1;
        } else {
            ans = num_stack.pop() + ans * op_stack.pop();
        }
    }
    return ans;
}

# 【模拟】还原排列的最少操作步数

给你一个偶数 n ，已知存在一个长度为 n 的排列 perm ，其中 perm[i] == i（下标从 0 开始计数）。

一步操作中，你将创建一个新数组 arr ，对于每个 i ：

如果 i % 2 == 0 ，那么 arr[i] = perm[i / 2] 如果 i % 2 == 1 ，那么 arr[i] = perm[n / 2 + (i - 1) / 2] 然后将 arr 赋值给 perm 。

要想使 perm 回到排列初始值，至少需要执行多少步操作？返回最小的非零操作步数。

// 输入：n = 2
// 输出：1
// 解释：最初，perm = [0,1]
// 第 1 步操作后，perm = [0,1]
// 所以，仅需执行 1 步操作

// 输入：n = 4
// 输出：2
// 解释：最初，perm = [0,1,2,3]
// 第 1 步操作后，perm = [0,2,1,3]
// 第 2 步操作后，perm = [0,1,2,3]
// 所以，仅需执行 2 步操作

// 方法一：直接模拟
const reinitialzePermutation = n => {
    let perm = new Array(n).fill(0).map((_, i) => i);
    let target = new Array(n).fill(0).map((_, i) => i);
    let step = 0;
    while(true) {
        let arr = new Array(n).fill(0);
        for(let i = 0; i < n; i++) {
            if((i & 1) !== 0) {
                arr[i] = perm[Math.floor(n / 2) + Math.floor((i - 1) / 2)];
            } else {
                arr[i] = perm[Math.floor(i / 2)];
            }
        }
        perm = arr;
        step++;
        if(perm.toString() === target.toString()) {
            break;
        }
    }
    return step
}

还原排列的最少操作步数 (opens new window)

# 逻辑思维

一个班级60%喜欢足球，70%喜欢篮球，80%喜欢排球，问即三种球都喜欢占比有多少？三个都喜欢的人数最多时，就尽量重复排列 60 70(10人喜欢一个) 70 80(现共有80人， 60人喜欢三个，10人喜欢两个， 10人喜欢一个)

所以10%- 60%

# 赛马

25匹马，5个赛道，求选出速度最快的3匹马最少需要多少次比赛？

7次由于场地只有5个赛道，每次最多5匹马比赛，将25匹马分为5组（A、B、C、D、E），每组5匹（编号1、2、3、4、5）。首先，进行5场比赛，每场比赛给每组排名。假设名次与编号一致，选出每组前三名。

25匹马，5个跑道，每个跑道最多能有1匹马进行比赛，最少比多少次能比出前3名？前5名？ (opens new window)

# 9个球问题

9个一样的球有一个和其他不同

# 转置矩阵

转置矩阵

# hw机试

# 字符串最大嵌套深度

// 力扣 ()
const maxDepth = function(s) {
    let ans = 0, size = 0;
    for(let i = 0; i < s.length; ++i) {
        const ch = s[i];
        if(ch === '(') {
            ++size;
            ans = Math.max(ans, size);
        } else if(ch === ')') {
            --size;
        }
    }
    return ans;
}

// 
function* items() {
    yield '([]{[()]})'
}
const nums = items();
const readline = () => {
    return nums.next().value
}
const fn = () => {
    const str = readline();
    // 判断是否是有效字符串 -- 单调栈
    const isValid = (s, n = 0) => {
        let stack = [];
        let nums = []
        for (let v of s) {
            if(!/\(|\)|\[|\]|\{|\}/.test(v)) return 0
            if(v === '('){
                stack.push(')');
                n++
            } else if(v === '['){
                stack.push(']');
                n++
            } else if(v === '{'){
                stack.push('}')
                n++
            } else {
                let char = stack.pop()
                s.includes(char) && n--
            }
            nums.push(n)
        }
        console.log(n)
        return n === 0 ? Math.max.apply(null, nums) : 0
    }
    n = isValid(str, 0) 
}
fn('([【】])')

参考字符串最大嵌套深度 (opens new window)

# 序号排序

function* items() {
    // yield 4'
    // yield '100 100 120 130' // 身高
    // yield '40 30 60 50' // 体重
    yield '3'
    yield '90 110 90' // 身高
    yield '45 60 45' // 体重
}
const nums = items();
const readline = () => {
    return nums.next().value
}
const fn = () => {
    let n = readline();
    let heights = readline().split(' ').map(n => Number(n));
    let tzs = readline().split(' ').map(n => Number(n));
    let persons = Array.from(Array(Number(n)), (_, i) => i + 1)
    let left = 0;
    while(left < persons.length) {
        let current = heights[left++];
        let right = left + 1;
        while(right < persons.length) {
            let rightNode = heights[right]
            if(rightNode < current) {
                swap(persons, left, right);
                swap(heights, left, right)
                swap(tzs, left, right)
            } else if(rightNode === current && tzs[right] < tzs[left]) {
                swap(persons, left, right);
                swap(heights, left, right)
                swap(tzs, left, right)
            }
            right++
        }
    }
    console.log(persons.join(' '))
}
const swap = (arr, i, j) => {
    [arr[i], arr[j]] = [arr[j], arr[i]]
}
fn();

# 图有向无权图单源最短路径问题

function* items() {
    yield '3 3'
    yield '1 2 11'
    yield '2 3 13'
    yield '1 3 50'
    yield '1 3' // 返回24
    // yield '([]{[()]})'
}
const nums = items();
const readline = () => {
    return nums.next().value
}
// 150 10: 30 无向图 表示 [{node: 1, target:2, time: 11}]
/**
 * 1- 3  50或24
 * nodes: [1, 2, 3]
 * [{node: 1, targets: [{node: 2, target:[3]}, {node: 3, target: null}]},]
 */
// 自己写的 ---有些问题
const fn = () => {
    let line = readline()
    const [n, m] = line.split(' '); // 节点个数n 时延列表的长度M
    let nodes = []
    let timesArr = []
    let maps = []
    for(let i = 0; i < m; i++) {
        let times = readline().split(' ')
        timesArr.push(times)
        nodes = nodes.concat([times[0], times[1]])
    }
    const [origin, target] = readline().split(' ');
    nodes = [...new Set(nodes)]
    for(let v of nodes) {
        let obj = {
            node: v,
            target: [],
            times: []
        }
        for (let m of timesArr) {
            if(m[0] === v) {
                obj.target.push(m[1])
                obj.times.push(m[2])
            }
        }
        maps.push(obj)
    }
    let result = [];
    let res = []
    findnodes(maps, origin, origin, target, result, res)
    console.log(Math.min.apply(null, res))
}
const findnodes = (maps, node, origin, target, result, res) => {
    for(let obj of maps) {  
        if(obj.node === node) {
            let index = obj.target.indexOf(target)
            if(index > -1) {
                result.push(obj.times[index])
                result = result.reduce((a, b) =>  Number(a) + Number(b), 0);
                res.push(result)
            } 
            obj.target.splice(index, 1)
            if(obj.target.length === 0) return res
            for (let [i, v] of obj.target.entries()) {
                findnodes(maps, v, origin, target, [obj.times[i]], res)
            }
        }
    }
}
fn();

LeetCode刷题16-最小传输时延 (opens new window)

华为OD机试真题（JavaScript） (opens new window)

# 句子相似性

// 输入：sentence1 = "My name is Haley", sentence2 = "My Haley"
// 输出：true
// 解释：可以往 sentence2 中 "My" 和 "Haley" 之间插入 "name is" ，得到 sentence1 。
const areSentencesSimilar = (sentence1, sentence2) => {
    let words1 = sentence1.split(' ');
    let words2 = sentence2.split(' ');

    if(words1.length === words.length) return sentence1 === sentence2;
    while(words1.length && words2.length && words1[words1.length - 1] === words2[words2.length - 1]) {
        words1.pop();
        words2.pop();
    }
    while(words1.length && words2.length && words1[0] === words2[0]) {
        words1.shift();
        words2.shift();
    }
    if(words1.length === 0 || words2.length === 0) return true;
    return false;
}

句子相似性 (opens new window)

# 统计一个数组中好对子的数目

给你一个数组 nums ，数组中只包含非负整数。定义 rev(x) 的值为将整数 x 各个数字位反转得到的结果。比方说 rev(123) = 321 ， rev(120) = 21 。我们称满足下面条件的下标对 (i, j) 是好的：

0 <= i < j < nums.length nums[i] + rev(nums[j]) == nums[j] + rev(nums[i]) 请你返回好下标对的数目。由于结果可能会很大，请将结果对 109 + 7 取余后返回。

// 输入：nums = [42,11,1,97]
// 输出：2
// 解释：两个坐标对为：
//  - (0,3)：42 + rev(97) = 42 + 79 = 121, 97 + rev(42) = 97 + 24 = 121 。
//  - (1,2)：11 + rev(1) = 11 + 1 = 12, 1 + rev(11) = 1 + 11 = 12 。
const countNicePairs = nums => {
    const MOD = 1e9 + 7;
    // 求rev翻转结果
    function rev(num) {
        let v = 0;
        while(num) {
            v = v * 10 + (num % 10);
            num = Math.floor(num / 10);
        }
        return v;
    }
    nums = nums.map(item => item - rev(item));
    // 公式转换nums[i] - rev(nums[i]) === nums[j] - rev(nums[j]);
    // 转换成求numsz中i< j 且nums[i] === nums[j];
    let ans = 0, map = new Map();
    for(let i = 0; i < nums.length; i++) {
        ans += (map.get(nums[i]) || 0) % MOD;
        ans = ans % MOD;
        map.set(nums[i], (map.get(nums[i]) || 0) + 1)
    }
    return ans;
}

# 其他

算法面试题汇总 (opens new window)

算法学习 (opens new window)

常见算法题 (opens new window)

leetcode练习题 →

# 牛客

# 找出数组的最大公约数

# 正则表达式匹配

# 两数之和

# 三数之和

# 快排

# 阮一峰老师的js快排实现

# 文章中提出的快排js实现

# 三、网上其他的快排js实现

# 二分查找

# 扑克牌问题

# 有A、B两个数组

# JavaScript 深拷贝

# 盛水最多的容器---双指针法

# 接雨水

# 大数相加--双指针

# sqrt---平方根

# 立方根

# [动态规划]恢复空格

# 两个数组的交集

# 统计字符串出现最多的字符

# 无重复字符的最长子串--单指针

# z-字形变换

# 查找一个字符中指定的子串的所有位置

# 缺失的第一个正数

# 寻找两个正序数组的中位数

# [数组]JS获取数组的所有子集---重要

# [数组]对角线遍历

# [数组]对角线遍历 II

# [数组]合并区间

# [数组]汇总区间

# [数组]缺失区间

# [数组]除自身以外的数组的乘积

# 数组中的第K个最大元素

# [数组]最大序数和/连续子数组的最大值

# [数组]长度最小的子数组(掌握滑动窗口&指针)

# [数组]分割数组最大值

# [数组]长度为k的最大子数组

# [数组]找到和最大的 长度为 K 的子序列

# [数组]-划分为k个相等的子集

# [数组-回溯]数组组合

# [数组-组合]下一个排列

# [数组]检查好数组

# 最长连续序列

# [动态规划]最长递增子序列

# [动态规划]最长递增序列的个数

# 字符串有效性检查

# 最长有效括号

# 括号的分数

# 使括号有效的最少添加(贪心)

# 会议室问题

# 加油站

# 山脉数组的峰顶索引

# 山脉数组中查找目标值

# 螺旋矩阵

# LRU 缓存机制

# [贪心]超级洗衣机

# [动态规划]编辑距离

# 单词接龙

# 所有子字符串美丽值之和

# N皇后

# 矩形重叠

# 矩形面积

# 最小面积矩形

# 柱状图中最大的矩形

# 岛屿数量

# 种花

# 鸡蛋掉落

# [拓扑]课程表

# 自除数

# 水仙花数

# 使绳子变成彩色的最短时间

# [滑动窗口]学生分数的最小差值

# 基本计算器

# 【模拟】还原排列的最少操作步数

# 逻辑思维

# 赛马

# 9个球问题

# 转置矩阵

# hw机试

# [数组]找到和最大的长度为 K 的子序列

# 图有向无权图单源最短路径问题