# 什么是动态规划
动态规划是求解决策过程最优化的数学方法。把多个过程转化成一些列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法-动态规划
# 什么时候要用动态规划
如果要求一个问题的最优化(通常是最大值或最小值),而且该问题能够**分解成若干个子问题,并且小问题之间也存在重叠的子问题,则考虑采用动态规划。
# 怎么使用动态规划
- 判断题意是否找出一个问题的最优解
- 从上往下分析问题,大问题可以分解成子问题,子问题中还有更小的子问题
- 从下往上分析,找出这些问题之间的关联(状态转移方程)
- 讨论底层的边界问题
- 解决问题(童男长使用数据进行迭代求出最优解)
# 最大子序和
给定一个整数数组nums,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和
输入: nums = [-2, 1, -3, 4, -1, 2,1, -5, 4]
输出:6
解释:连续子数组[4, -1, 2, 1]的和最大为6

var maxSubArray = function(nums) {
var cur = 0; maxSub = nums[0];
nums.forEach(x => {
cur = Math.max(cur + x, x);
maxSub = Math.max(maxSub, cur);
})
return maxSub;
};
# 爬楼梯
var climbStairs = function(n) {
var dp = [];
dp[0] = 1;
dp[1] = 1;
for (var i = 2; i <= n; i++) {
dp[i] = dp[i - 1] + dp[i - 2]
}
return dp[n];
}
# 最长回文串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
定义状态 dp[i][j]表示子串s[i...j]是否为回文串,这里子串s[i..j]定义为左闭右闭区间,可以取到s[i]和s[j]。
思考状态转移方程 对于一个子串而言,如果它是回文串,那么它的收尾增加一个相同字符,它仍然是个回文串
dp[i][j] = (s[i] === s[j]) && dp[i + 1][j - 1]初始状态
dp[i][j] = true // 单个字符是回文串 if(s[i] === s[s+1]) dp[i][i+ 1] = true; // 连续两个相同字符是回文串代码实现
const logestPalindrome = s => {
if (s.length < 2) return s;
let res = s[0], dp = Array.from(Array(s.length), () => Array(s.length).fill(0))
for (let i = 0; i < s.length; i++) {
dp[i][i] = true;
}
for (let j = 1; j < s.length;; j++) {
for (let i = 0; i < j; i++) {
if (j - i === 1 && s[i] === s[j]) {
dp[i][j] = true;
} else if (s[i] === s[j] && dp[i+ 1][j - 1]) {
dp[i][j] = true;
}
// 获取当前最长回文子串
if(dp[i][j] && j - i + 1 > res.length) {
res = s.substring(i, j+ 1);
}
}
}
return res;
}
// 第二种
var longestPalindrome = function(s) {
let ans = '';
let n = s.length;
let dp = Array.from(Array(n), (_, i) => Array(n).fill(0));
for(let i = n-1; i >=0; i--) {
for (let j = i; j < n; j++) {
dp[i][j] = s[i] === s[j] && ( j - i < 2 || dp[i+1][j-1])
if (dp[i][j] && j - i + 1 > ans.length) {
ans = s.substr(i, j - i + 1)
}
}
}
return ans;
};
// 第三种
const LongReverseStr = str => {
let ans = '';
let len = str.length;
let dp = Array.from(Array(len + 1), (_, i) => Array(len + 1).fill(true));
for(let i = 1; i <= len; i++) {
for(let j = 1; j <= len; j++) {
dp[i][j] = str[i] === str[j] && (j - i < 2 || dp[i - 1][j - 1])
if(dp[i][j] && j - i + 1 > ans.length) {
ans = str.substr(i, j - i + 1)
}
}
}
console.log(dp)
return ans;
}
console.log(LongReverseStr('babad'))
复杂度分析:
时间复杂度:O(n^2^)
空间复杂度:O(n^2^)
# 分割回文串
给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
回文串 是正着读和反着读都一样的字符串。
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
解答
const partition = s => {
const dfs = (i) => {
if (i === n) {
ret.push(ans.slice());
return;
}
for (let j = i; j < n; ++j) {
if (f[i][j]) {
ans.push(s.slice(i, j + 1));
dfs(j + 1);
ans.pop();
}
}
}
// const n = s.length;
// const f = new Array(n).fill(0).map(() => new Array(n).fill(true));
// let ret = [], ans = [];
// for (let i = n - 1; i >= 0; --i) {
// for (let j = i + 1; j < n; ++j) {
// f[i][j] = (s[i] === s[j]) && f[i + 1][j - 1];
// }
// }
const n = s.length;
const f = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(true));
let ret = [], ans = [];
for(let i = 1; i <= n; i++) {
for(let j = 1; j <= n; j++) {
f[i][j] = s[i] === s[j] && f[i - 1][j - 1]
}
}
dfs(0);
return ret;
}
# 单词划分
输入: s = "leetcode", wordDict = ["leet", "code"]
输出: true
解释: 返回 true 因为 "leetcode" 可以由 "leet" 和 "code" 拼接成。
解答
var wordBreak = function(s, wordDict) {
const wordSet = new Set(wordDict);
const len = s.length;
const dp = new Array(len + 1).fill(false);
dp[0] = true;
for (let i = 1; i <= len; i++) {
for (let j = i - 1; j >= 0; j--) {
if (dp[i] === true) break;
if (dp[j] === false) continue;
const suffix = s.slice(j, i);
if (wordSet.has(suffix) && dp[j] = true) {
dp[i] = true;
break;
}
}
}
return dp[s.length]
}
# 割绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长的 m 段( m 、 n 都是整数, n > 1 并且 m > 1 , m <= n ),每段绳子的长度记为 k[1],...,k[m] 。请问 k[1]k[2]...*k[m] 可能的最大乘积是多少?例如,当绳子的长度是 8 时,我们把它剪成长度分别为 2、3、3 的三段,此时得到的最大乘积是 18 。
var cuttingRope = function(n) {
let i, j, dp = new Array(n + 1).fill(0), nowBigger;
dp[2] = 1;
// 如果只剪掉长度为1,对最后的乘积无任何增益,所以从长度为2开始剪
for(i = 2; i <= n; i++) {
for(j = 1; j < i; j++) {
// 剪了第一段后,剩下(i - j)长度可以剪也可以不剪。如果不剪的话长度乘积即为j * (i - j);如果剪的话长度乘积即为j * dp[i - j]。取两者最大值
nowBigger = Math.max(j * (i - j), j * dp[i - j]);
// 对于同一个i,内层循环对不同的j都还会拿到一个max,所以每次内层循环都要更新max
dp[i] = Math.max(dp[i], nowBigger);
}
}
return dp[n];
};
# 最长公共子序列
输入:text1 = "abcde", text2 = "ace"
输出:3
解释:最长公共子序列是 "ace" ,它的长度为 3 。
解答
const longestCommonSubsequence = (str1, str2) => {
let n = str1.length;
let m = str2.length;
let dp = Array.from(Array(n + 1), (_, i) => Array(m + 1).fill(0));
for(let i = 1; i <= n; i++) {
let c1 = str1[i - 1];
for(let j = 1; j <= m; j++) {
let c2 = str2[j - 1];
if(c1 === c2) {
dp[i][j] = dp[i - 1][j - 1] + 1
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1])
}
}
}
return dp[n][m]
}
# 礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
const maxValue = grid => {
let n = grid.length;
let m = grid[0].length;
let dp = Array.from(Array(n), (_, i) => Array(m).fill(0));
dp[0][0] = grid[0][0]
for(let i = 0; i < n; i++) {
for(let j = 0; j < m; j++) {
if(i === 0 && j == 0) continue;
if(i == 0) dp[i][j] = dp[i][j - 1] + grid[i][j];
if(j == 0) dp[i][j] = dp[i - 1][j] + grid[i][j]
if(i !== 0 && j !== 0) dp[i][j] = Math.max(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j])
}
}
return dp[n - 1][m - 1]
}
# 规划兼职工作
输入:startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
输出:120
解释:
我们选出第 1 份和第 4 份工作,
时间范围是 [1-3]+[3-6],共获得报酬 120 = 50 + 70。
const jobScheduling = (startTime, endTime, profit) => {
const n = startTime.length;
const jobs = new Array(n).fill(0).map((_, i) => [startTime[i], endTime[i], profit[i]]);
const dp = new Array(n + 1).fill(0);
for (let i = 1; i <= n; i++) {
const k = binarySearch(jobs, i - 1, jobs[i - 1][0]);
dp[i] = Math.max(dp[i - 1], dp[k] + jobs[i - 1][2]);
}
return dp[n];
}
const binarySearch = (jobs, right, target) => {
let left = 0;
while (left < right) {
const mid = left + Math.floor((right - left) / 2);
if (jobs[mid][1] > target) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
# 火柴拼正方形
// 状态压缩+动态规划
const makesquare = function(matchsticks) {
const totalLen = matchsticks.reduce((acc, cur) => acc + cur)
if(totalLen % 4 !== 0) return false;
const len = Math.floor(totalLen / 4), n = matchsticks.length;
const dp = new Array(1 << n).fill(-1);
dp[0] = 0;
for (let s = 1; s < (1 << n); s++) {
for (let k = 0; k < n; k++) {
if ((s & (1 << k)) === 0) {
continue;
}
const s1 = s & ~(1 << k);
if (dp[s1] >= 0 && dp[s1] + matchsticks[k] <= len) {
dp[s] = (dp[s1] + matchsticks[k]) % len;
break;
}
}
}
return dp[(1 << n) - 1] === 0;
}
console.log(makesquare([1,1,2,2,2])) // true
# 跳跃游戏
// 输入:nums = [2,3,1,1,4]
// 输出:true
// 解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
// 由题目描述,我们需要达到最后一个下标,那么最后一个下标的数字其实是可以不用考虑的。那么我们可以假设只有两个数字(比如 [2,4][2, 4][2,4]),这个时候第一个数字如果是大于等于 111 的数就成立;如果是三个数字的话(比如 [3,0,4][3, 0, 4][3,0,4]),第一个数字大于等于 222 时成立。依此类推,一个数字可以到达的位置必须是这个数字标记的长度值,有:nums[i]>=jnums[i] >= jnums[i]>=j 成立时才可以到达后面第 jjj 个目标。
const canJump = function(nums) {
let end = nums.length - 1;
for(let i = nums.length - 2; i >= 0 i--) {
if(end - i <= nums[i]) {
end = i;
}
}
return end === 0;
}
// 贪心算法
// 从当前位置能够到达某一个位置,那么从当前位置都可以到达某一位置左侧的所有位置
// 根据这个原则,只要从第一个位置开始逐步找能跳跃最远的位置,如果这个位置正好在最后一个下标或超过最后一个下标,那么一定能到达最后一个下标
var canJump = nums => {
let n = nums.length - 1;
let maxLen = 0;
for(let i = 0; i <= maxLen; i++) {
maxLen = Math.max(maxLen, nums[i] + 1);
if(maxLen >= n) return true;
}
return false;
}
# 最长斐波那契数列
// 输入: arr = [1,2,3,4,5,6,7,8]
// 输出: 5
// 解释: 最长的斐波那契式子序列为 [1,2,3,5,8] 。
const lenLongestFibSubseq = arr => {
const indices = new Map();
const n = arr.length;
for(let i = 0; i < n; i++) {
indices.set(arr[i], i)
}
const dp = new Array(n).fill(0).map(() => new Array(n).fill(0));
let ans = 0;
for(let i = 0; i < n; i++) {
for(let j = n - 1; j >= 0; j--) {
if(arr[j] * 2 <= arr[i]) break;
if(indices.has(arr[i] - arr[j])) {
const k = indices.get(arr[i] - arr[j]);
dp[j][i] = Math.max(dp[k][j] + 1, 3);
ans = Math.max(ans, dp[j][i])
}
}
}
return ans;
}
# 堆叠长方体的最大高度
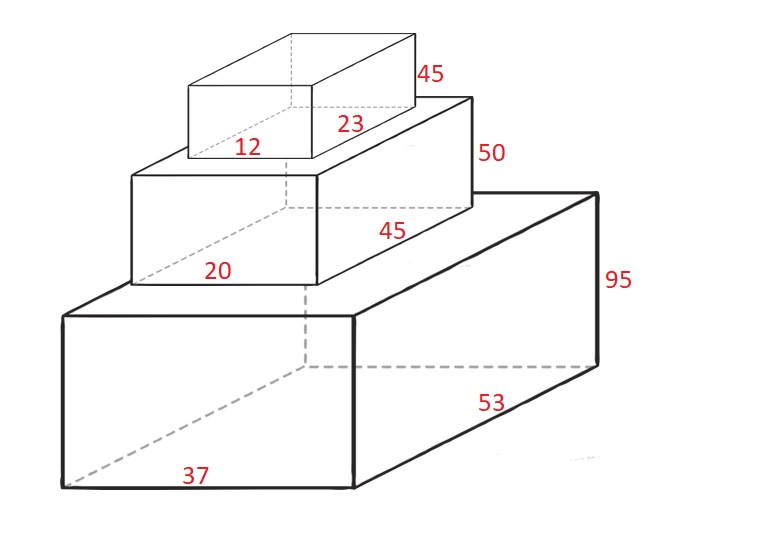
// 输入:cuboids = [[50,45,20],[95,37,53],[45,23,12]]
// 输出:190
// 解释:
// 第 1 个长方体放在底部,53x37 的一面朝下,高度为 95 。
// 第 0 个长方体放在中间,45x20 的一面朝下,高度为 50 。
// 第 2 个长方体放在上面,23x12 的一面朝下,高度为 45 。
// 总高度是 95 + 50 + 45 = 190 。
const maxHeight = function(cuboids) {
let n = cuboids.length;
for(const v of cuboids) {
v.sort((a, b) => a - b);
}
cuboids.sort((a, b) => (a[0] + a[1] + a[2]) - (b[0] + b[1] + b[2]));
let ans = 0;
let dp = new Array(n).fill(0);
for(let i = 0; i < n; i++) {
dp[i] = cuboids[i][2];
for(let j = 0; j < i; j++) {
if(cuboids[i][0] >= cuboids[j][0] &&
cuboids[i][1] >= cuboids[j][1] &&
cuboids[i][2] >= cuboids[j][2]
) {
dp[i] = Math.max(dp[i], dp[j] + cuboids[i][2]);
}
}
ans = Math.max(ans, dp[i]);
}
return ans;
}
# 最小路径
const minPath = grid => {
let row = grid.length;
let col = grid[0].length;
for(let i = 1; i < row; i++) {
grid[i][0] += grid[i - 1][0]
}
for(let j = 1; j < col; j++) {
grid[0][j] += grid[0][j - 1];
}
for(let i = 1; i < row; i++) {
for(let j = 1; j < col; j++) {
grid[i][j] += Math.min(grid[i - 1][j], grid[i][j - 1]);
}
}
return grid[row - 1][col - 1];
}
# 剑指 Offer 47. 礼物的最大价值--经典
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
// 输入:
// [
// [1,3,1],
// [1,5,1],
// [4,2,1]
// ]
// 输出: 12
// 解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
const maxValue = function(grid) {
let n = grid.length;
let m = grid[0].length;
let dp = Array.from(Array(n), (_, i) => Array(m).fill(0));
for(let i = 0; i < n; i++) {
for(let j = 0; j < m; j++) {
if(i === 0 && j === 0) continue;
if(j === 0) dp[i][j] = dp[i][j - 1] + grid[i][j];
f(j == 0) dp[i][j] = dp[i - 1][j] + grid[i][j]
if(i !== 0 && j !== 0) dp[i][j] = Math.max(dp[i - 1][j] + grid[i][j], dp[i][j - 1] + grid[i][j])
}
}
return dp[n - 1][m - 1]
}