# 二叉树
是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树
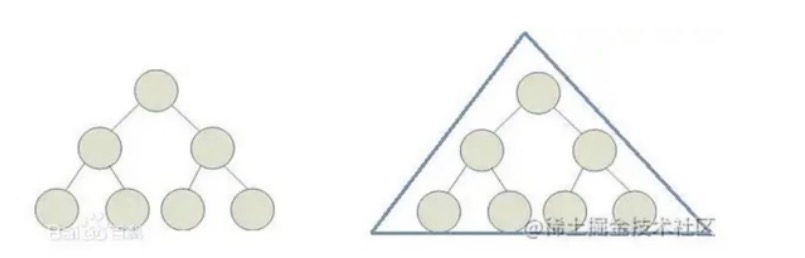
# 满二叉树
除最后一层无任何子节点外,每一层上的所有节点都有两个子节点的二叉树。
从图形形态上看,满二叉树是一个三角形。
如果一个二叉树的层数为K,且节点总数是(2^K) - 1, 则它是满二叉树
TIP
注意:关于满二叉树定义里,国内外定义有分歧,本文采用的是国内定义。满二叉树英文是Full Binary Tree,是指所有的节点的度只能是0或者2, 如下图,国外也为人是Full Binary Tree

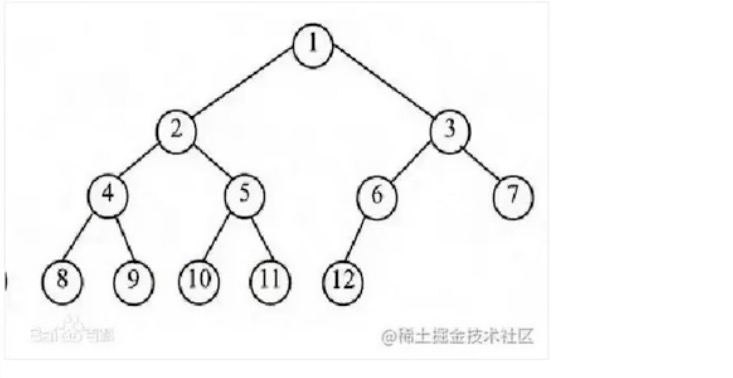
# 完全二叉树
一颗深度为K的有n个节点的二叉树,对树中的节点按照从上到下、从左到右的顺序进行编号,如果编号为i(1<= i<=n)的节点与满二叉树中编号为i的节点在二叉树中的位置相同,则这颗二叉树成为完全二叉树。叶子节点只可能在最大的两层出现
# 二叉搜索树
# 特点
- 若左子树不为空,则左子树上所有节点的值均小于它的根节点的值
- 若右子树不为空,则右子树上所有节点的值均大于等会它的根节点的值
- 左、右树也分别为二叉排序树
也就是说,二叉查找树,左子树都都比节点小,右子树都比节点大,递归定义
根据二叉排序树这个特点我们可以知道:二叉排序树的中序遍历一定是从小到大的
比如上图,中序遍历结果是:
1 3 4 6 7 8 10 13 14
搞定二叉搜索树,9图足矣! (opens new window)
# 平衡二叉树(AVL树)
平衡二叉树是任何两个子树的高度差不超过1(平衡因子)的二叉树(可以是空树)
平衡而出为了保持"完全平衡",当由于增删数据发生不平衡时,会通过旋转达到平衡的目的。旋转方式
左转
右转
# 红黑树
红黑树是一种含有红黑节点,并能自平衡的二叉查找树。红黑树必须具有一下特性:
- 所有节点必须是红色或者黑色
- 根节点必须是黑色
- 所有叶子节点(NIL)d都是黑色
- 每个红色节点的两个子节点一定都是黑色
- 每个节点到叶子节点的路径上,都包含相同数量的黑色节点
- 如果一个节点为黑色,那么这个节点一定有两个子节点
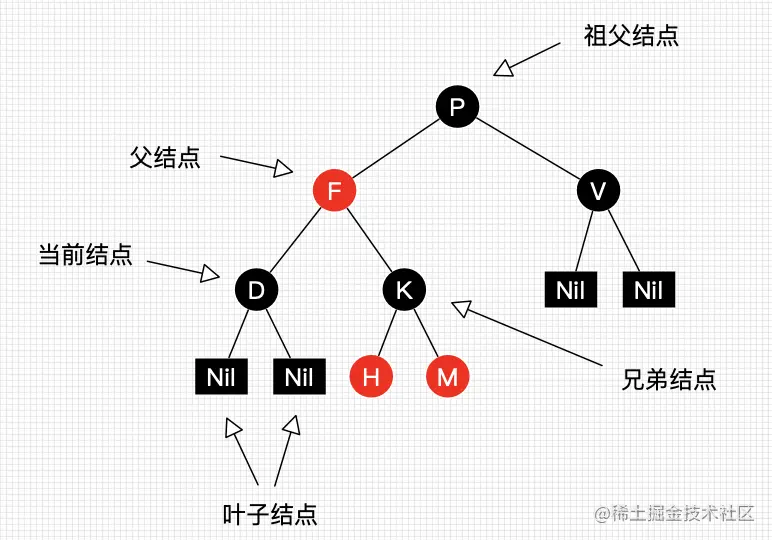
红黑树是一种完全平衡的二叉查找树,如图,根节点的左子树明显比右子树高,但是左子树和右子树的黑色节点的层数是相等的,即属性5。每次添加、删除节点,红黑树会通过旋转和变色来保持自平衡,且旋转次数最多为3,复杂度是O(lgn)。
# 遍历方法
- 层序遍历
- 递归(一般用于深度优先 也可以层序遍历)