
# 前言
- 优先队列
- 图
- 前缀树
- 线段树
- 树状数组
# 优先队列
# 与普通队列的区别
- 保证每次取出的元素是队列中优先级最高的
- 优先级别可自定义

# 常用的场景
- 从杂乱无章的数据中按照一定的顺序(或者优先级)刷选数据
# 本质
二叉堆结构,堆在英文里叫Binary Heap
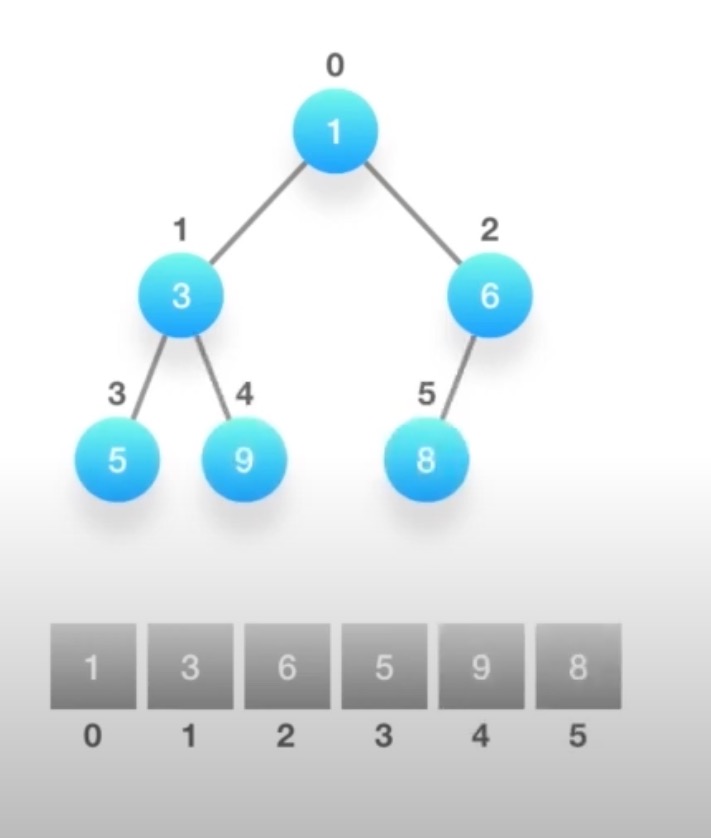
利用一个数组结构来实现完全二叉树
# 特性
数组里的每一个元素array[0]拥有最高的优先级,给定一个下标i,那么对于元素array[i]而言
- 父节点对应的下标是(i - 1) / 2;
- 右侧子节点对应的元素下标是2 * i+ 1;
- 左侧对应的元素的下标是 2* i + 2; 数组中每个元素的优先级都必须要高于两侧的子节点
# 其基本操作为一下两个
- 向上筛选--新增节点放在最后,沿着节点向上爬
- 向下筛选- 不断执行向下筛选的操作,该元素和它的两个孩子节点对比,发现那个优先级别最高,如果孩子节点级别高,然后直接交换;沿着树的高度往下爬
** 另一个重要的时间复杂度:优先队列初始化(O^n)**
# 前K个高频元素

# 图
最基本的知识点如下
- 阶、度(出度,入度)
- 树、森林、环
- 有向图、无向图、完全有向图、完全无向图
- 连通图、连通分量
- 图的存储和表达方式:邻接矩阵、邻接链表
TIP
- 度: 某个定点的度就是依附于该定点的变得个数
- 环:是一条至少含有一条边且终点和起点相同的路径
- 路径:是由边顺序连接的一系列的顶点组成
- 子图:是一幅图的所有边的子集(包含这些边依附的顶点)组成的图
- 相邻定点:当两个定点通过一条边相连时,我们称这两个定点是相邻的,并且称这条边依附于这两个顶点
围绕图的算法也是各式各样
- 图的遍历:深度优先、广度优先
- 环的检测:有向图、无向图
- 拓扑排序
- 最短路径算法
- 连通性相关算法: Kosarauju、Tarjan、求解孤岛的数量、判断是否为树
- 图的着色、旅行商问题等
必须熟练掌握的知识点
- 图的存储和表达方式:邻接矩阵、邻接链表
- 图的遍历:深度优先、广度优先
- 二部图的检测、树的检测、环的检测:有向图、无向图
- 拓扑排序
- 联合-查找算法
- 最短路径
# 图的存储结构
要表示一幅图,只需要表示清楚一下两个部分内容即可
- 图中所有的顶点
- 所有连接顶点的边
常见的图的存储结构有两种:邻接矩阵和邻接表
# 邻接矩阵
二维数组---二维数组索引表示顶点,二维数组的值表示边
缺点-- 占用内容空间是n^2,如果我们处理的问题规模比较大的话 内存空间可能不够用
# 邻接表
数组--数组的每个值存储的是队列对象(queue对象); 数组索引表示图的顶点 值表示与索引相邻的顶点
邻接表的空间并不是线性级别的 性能好于邻接矩阵
# 判断二分图

# 前缀树
也称字典树
这种数据结构被广泛地运用在字典查询当中
什么是字典查找?
例如:给定一系列构成字典的字符串,要求在字典当中找出所有以『ABC』开头的字符串
- 暴露搜索法 --- O(M * n)
- 前缀树--O(m)
# 经典应用
搜索框输入搜索文字,会罗列以搜索词开头的相关搜索
汉字拼音输入法
# 重要性质
每个节点至少包含两个基本属性
- children:数组或者集合,罗列出每个分支当中包含的所有字符
- isEnd:布尔值,表示该节点是否为某字符串的几位
根节点是空的--只利用节点的children属性
除了根节点,其他所有节点都可能是单词的结尾,叶子节点一定都是单词的结尾
# 基本操作
- 创建
方法
遍历一遍输入的字符串,对每个字符串的字符进行遍历
从前缀树的根节点开始,将每个字符加入到节点的childrend字符集当中
如果字符集已经包含了这个字符,跳过
如果当前字符是字符串的最后一个,把当前节点的isEnd标记为真
- 搜索
从前缀树的根节点触发,逐个匹配输入的前缀字符
如果遇到了,继续下一层搜索
# 单词搜索贰


# 线段树
# 一个例题
假设我们有一个数组array[0...n - 1],里面有n个元素,现在我们要经常对这个数组做两个事
- 更新数组元素的数值
- 求数组任意一段去区间里元素的总和(或者平均值)
- 方法一:遍历一遍数组 (O(n))
- 线段树(O(logn))
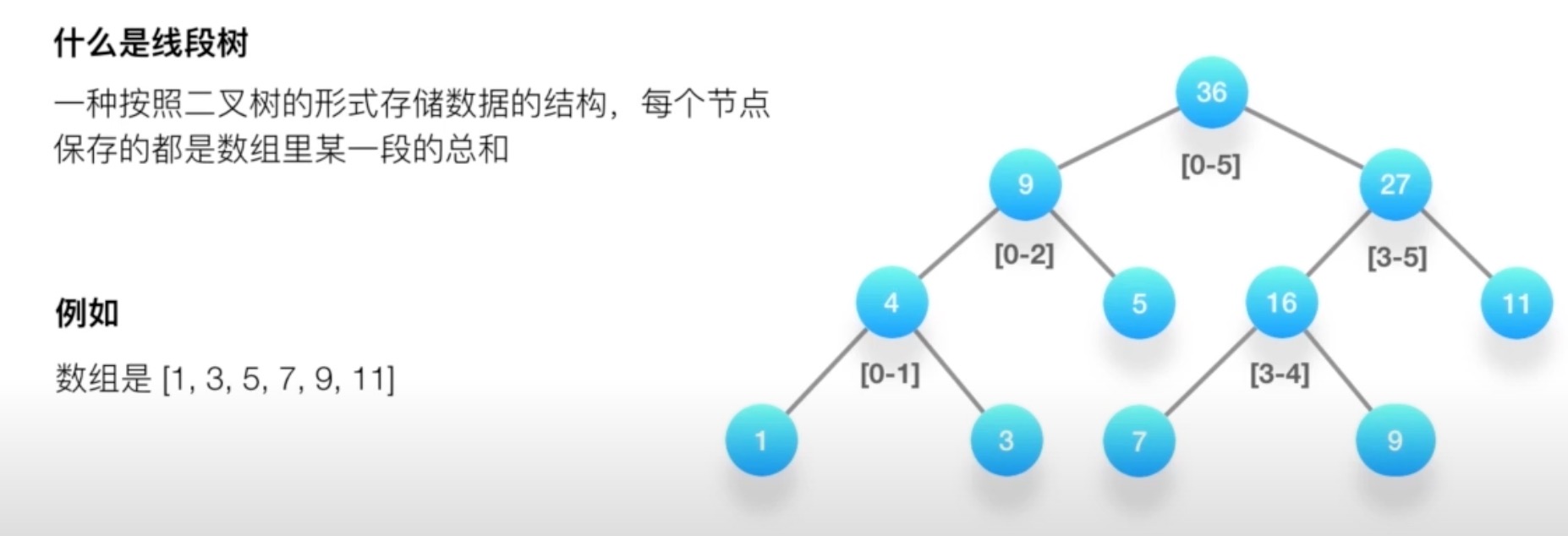
# 什么是线段树
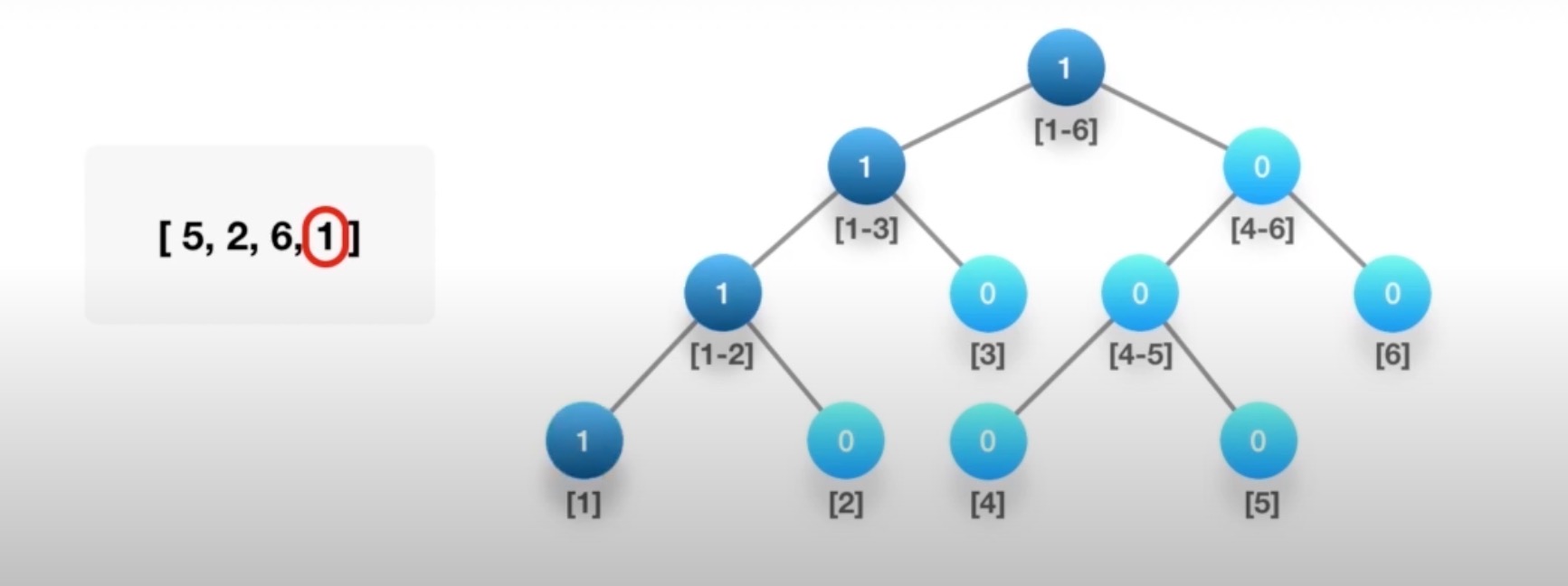
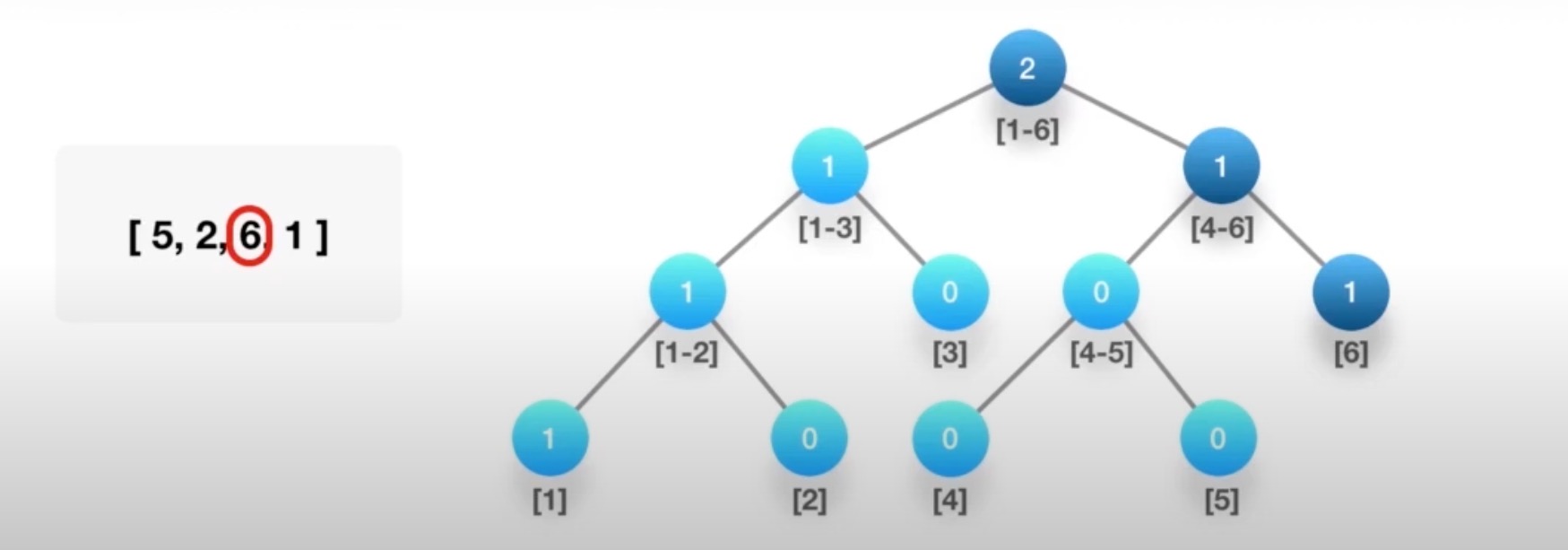
# 计算右侧小宇当前元素的个数

判断在那个区间,对应区间+1
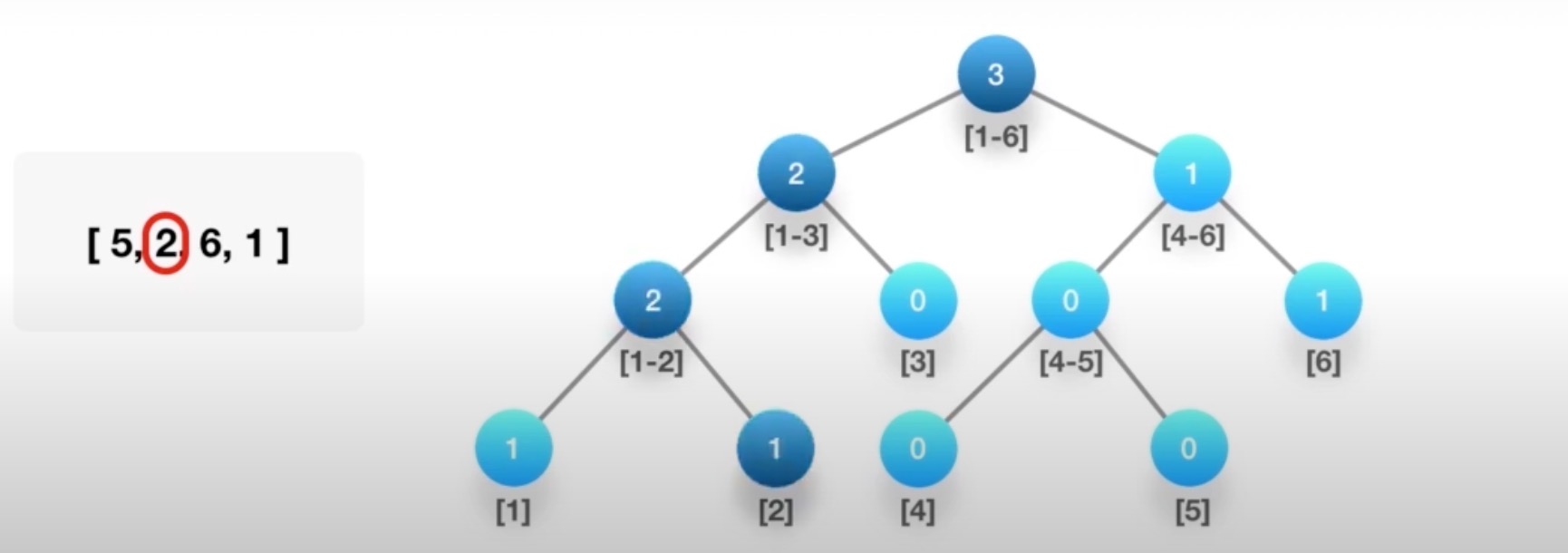
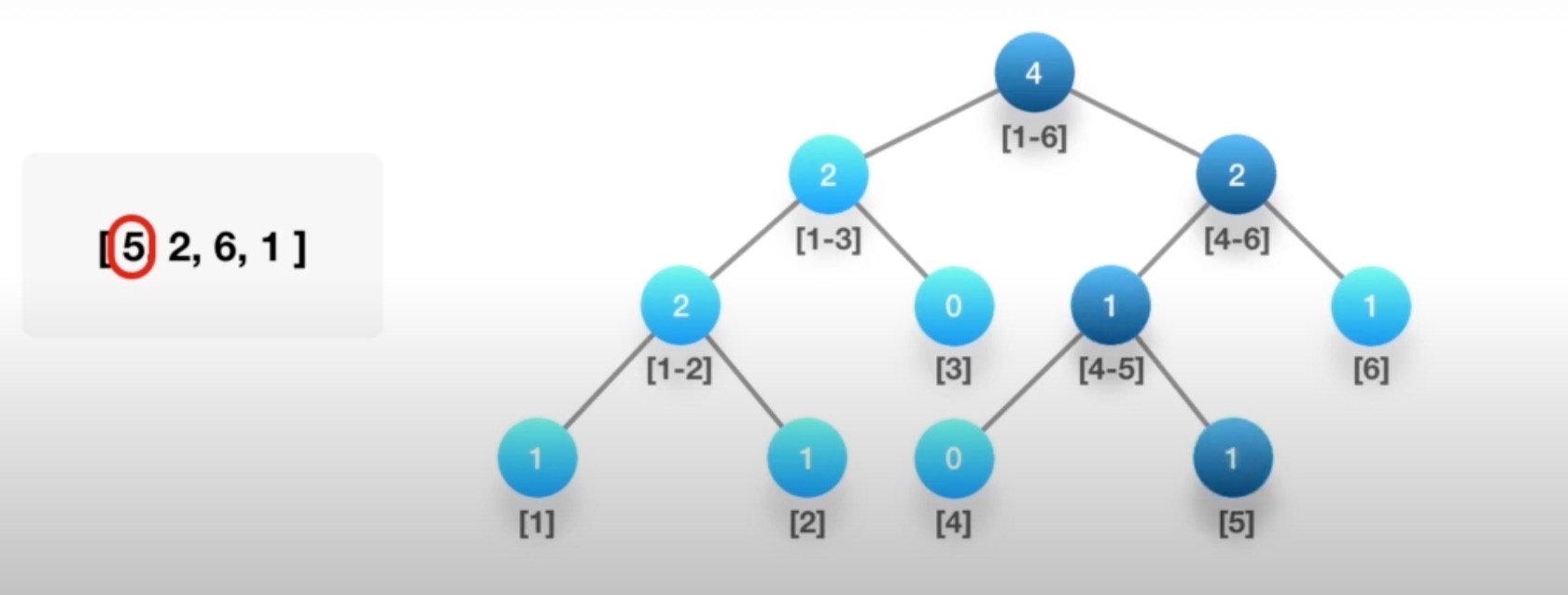
# 树状数组
# 一个例题
假设我们有一个数组array[0...n -1],里面有n个元素,我们要经常对这个数组做两件事
- 更新数组元素的数组
- 求数组前K个元素总和(或平均值)
- 线段树(Ologn)
- 树状数组(Ologn)
# 重要的基本特征
利用数组来表述多叉树的结构,和优先队列有些类似
优先队列是用数组来表示完全二叉树,而树状数组是多叉树
树状数组的第一个元素是空节点
如果节点tree[k]是tree[x]的父节点,那么需要满足y= x - (x & (-x))
# 结束
